Page 775 - Advanced_Engineering_Mathematics o'neil

23.1 Conformal Mappings 755

z w z L 2
C 2 Tangent to f(C ) w
2
f(L )
Tangent to C 2 2
θ θ f(C 2 ) L 1
Tangent to C 1 Tangent to f(L )
1
f(C )
1
C 1 f(C 1 )

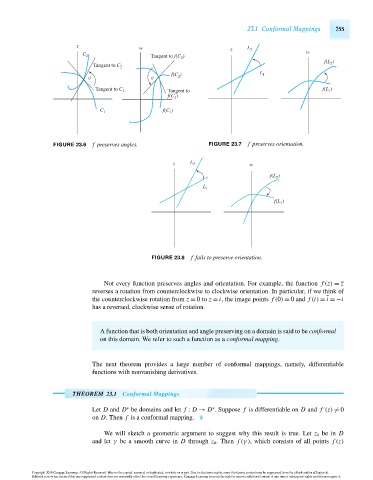
FIGURE 23.6 f preserves angles. FIGURE 23.7 f preserves orientation.

z L 2 w

f(L )
2
L 1
f(L )
1

FIGURE 23.8 f fails to preserve orientation.

Not every function preserves angles and orientation. For example, the function f (z) = z
reverses a rotation from counterclockwise to clockwise orientation. In particular, if we think of
the counterclockwise rotation from z = 0to z = i, the image points f (0) = 0 and f (i) = i =−i
has a reversed, clockwise sense of rotation.

A function that is both orientation and angle preserving on a domain is said to be conformal
on this domain. We refer to such a function as a conformal mapping.

The next theorem provides a large number of conformal mappings, namely, differentiable
functions with nonvanishing derivatives.

THEOREM 23.1 Conformal Mappings

Let D and D be domains and let f : D → D . Suppose f is differentiable on D and f (z) = 0

∗
∗
on D. Then f is a conformal mapping.
We will sketch a geometric argument to suggest why this result is true. Let z 0 be in D
and let γ be a smooth curve in D through z 0 . Then f (γ ), which consists of all points f (z)

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 15:39 THM/NEIL Page-755 27410_23_ch23_p751-788