Page 28 - Advanced engineering mathematics

8 CHAPTER 1 First-Order Differential Equations

x
–1 0 1 2 3

–0.4

–0.8
y

–1.2

–1.6

–2

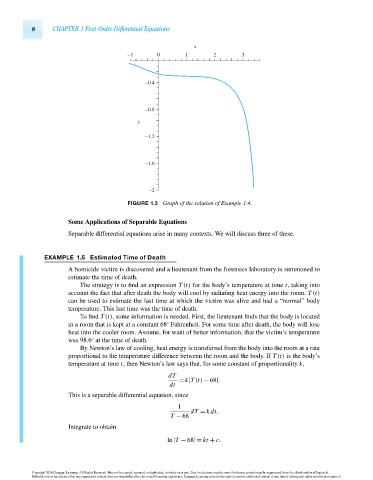
FIGURE 1.3 Graph of the solution of Example 1.4.

Some Applications of Separable Equations

Separable differential equations arise in many contexts. We will discuss three of these.

EXAMPLE 1.5 Estimated Time of Death
A homicide victim is discovered and a lieutenant from the forensics laboratory is summoned to
estimate the time of death.
The strategy is to find an expression T (t) for the body’s temperature at time t, taking into
account the fact that after death the body will cool by radiating heat energy into the room. T (t)
can be used to estimate the last time at which the victim was alive and had a “normal” body
temperature. This last time was the time of death.
To find T (t), some information is needed. First, the lieutenant finds that the body is located
in a room that is kept at a constant 68 Fahrenheit. For some time after death, the body will lose
◦
heat into the cooler room. Assume, for want of better information, that the victim’s temperature
was 98.6 at the time of death.
◦
By Newton’s law of cooling, heat energy is transferred from the body into the room at a rate
proportional to the temperature difference between the room and the body. If T (t) is the body’s
temperature at time t, then Newton’s law says that, for some constant of proportionality k,
dT
= k[T (t) − 68].
dt
This is a separable differential equation, since
1
dT = kdt.
T − 68
Integrate to obtain

ln|T − 68|= kt + c.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:9 THM/NEIL Page-8 27410_01_ch01_p01-42