Page 283 - Advanced engineering mathematics

8.6 The Matrix Tree Theorem 263

V

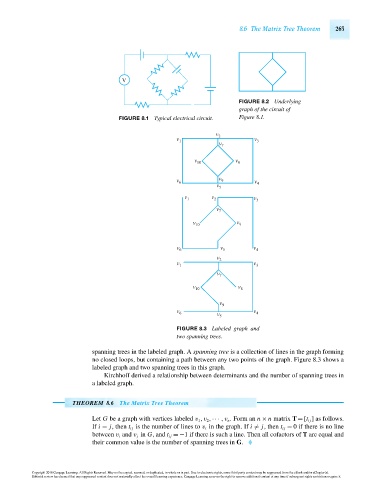
FIGURE 8.2 Underlying
graph of the circuit of
FIGURE 8.1 Typical electrical circuit. Figure 8.1.

v 2
v 1 v 3
v 7

v 10 v 8

v 9
v 6 v 4
v 5
v 1 v 2
v 3
v 7
v
v 10 9

v 6 v 5 v 4
v 2
v 1 v 3

v 7
v 10 v 8

v 9
v 6 v 5 v 4

FIGURE 8.3 Labeled graph and
two spanning trees.

spanning trees in the labeled graph. A spanning tree is a collection of lines in the graph forming
no closed loops, but containing a path between any two points of the graph. Figure 8.3 shows a
labeled graph and two spanning trees in this graph.
Kirchhoff derived a relationship between determinants and the number of spanning trees in
a labeled graph.

THEOREM 8.6 The Matrix Tree Theorem

Let G be a graph with vertices labeled v 1 ,v 2 ,··· ,v n .Forman n × n matrix T =[t ij ] as follows.
If i = j, then t ij is the number of lines to v i in the graph. If i = j, then t ij = 0ifthereisnoline
between v i and v j in G, and t ij =−1 if there is such a line. Then all cofactors of T are equal and
their common value is the number of spanning trees in G.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:26 THM/NEIL Page-263 27410_08_ch08_p247-266