Page 397 - Advanced engineering mathematics

12.3 An Extension of Green’s Theorem 377

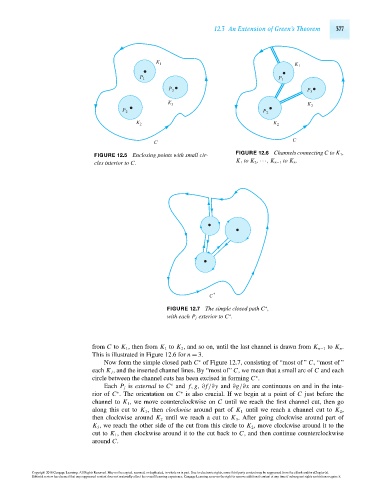
K 1 K 1

P 1 P 1
P 3 P 3

K 3 K 3
P 2 P 2
K 2 K 2

C
C
FIGURE 12.5 Enclosing points with small cir- FIGURE 12.6 Channels connecting C to K 1 ,
K 1 to K 2 , ···,K n−1 to K n .
cles interior to C.

C *

FIGURE 12.7 The simple closed path C ,
∗
with each P j exterior to C .
∗

from C to K 1 , then from K 1 to K 2 , and so on, until the last channel is drawn from K n−1 to K n .
This is illustrated in Figure 12.6 for n = 3.
∗
Now form the simple closed path C of Figure 12.7, consisting of “most of ” C,“mostof ”
each K j , and the inserted channel lines. By “most of” C, we mean that a small arc of C and each
circle between the channel cuts has been excised in forming C .
∗
Each P j is external to C and f, g, ∂ f/∂y and ∂g/∂x are continuous on and in the inte-
∗
rior of C . The orientation on C is also crucial. If we begin at a point of C just before the
∗
∗
channel to K 1 , we move counterclockwise on C until we reach the first channel cut, then go
along this cut to K 1 , then clockwise around part of K 1 until we reach a channel cut to K 2 ,
then clockwise around K 2 until we reach a cut to K 3 . After going clockwise around part of
K 3 , we reach the other side of the cut from this circle to K 2 , move clockwise around it to the
cut to K 1 , then clockwise around it to the cut back to C, and then continue counterclockwise
around C.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:53 THM/NEIL Page-377 27410_12_ch12_p367-424