Page 56 - Advanced engineering mathematics

36 CHAPTER 1 First-Order Differential Equations

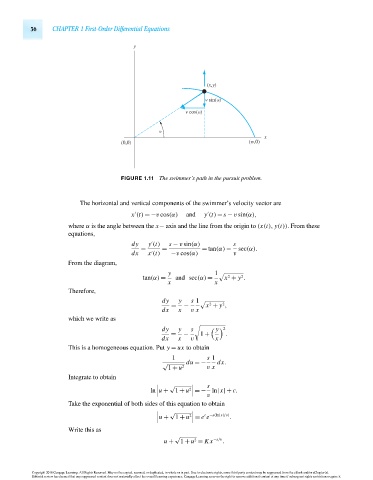
y

(x,y)

v sin(α)
v cos(α)

α
x
(0,0) (w,0)

FIGURE 1.11 The swimmer’s path in the pursuit problem.

The horizontal and vertical components of the swimmer’s velocity vector are

x (t) =−v cos(α) and y (t) = s − v sin(α),
where α is the angle between the x− axis and the line from the origin to (x(t), y(t)). From these
equations,
dy y (t) s − v sin(α) s

= = = tan(α) − sec(α).
dx x (t) −v cos(α) v

From the diagram,
y 1
2
2
tan(α) = and sec(α) = x + y .
x x
Therefore,
dy y s 1
2
2
= − x + y ,
dx x v x
which we write as

y
dy y s
2
= − 1 + .
dx x v x
This is a homogeneous equation. Put y = ux to obtain
1 s 1
√ du =− dx.
1 + u 2 v x
Integrate to obtain
√ s
2

ln u + 1 + u =− ln|x|+ c.

v
Take the exponential of both sides of this equation to obtain
√
c −s(ln|x|/v)
2

u + 1 + u = e e .

Write this as
√
2
u + 1 + u = Kx −s/v .
Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.
October 14, 2010 14:9 THM/NEIL Page-36 27410_01_ch01_p01-42