Page 57 - Advanced engineering mathematics

1.5 Additional Applications 37

To solve this for u, first write
√
1 + u = Kx −s/v − u
2
and square both sides to obtain
2
2
2
1 + u = K x −2s/v + u − 2Kux −s/v .
2
Now u cancels, and we can solve for u to obtain
1 1 1
u(x) = Kx −s/v − x s/v .
2 2 K
Finally, u = y/x,so
1 1 1
y(x) = Kx 1−s/v − x 1+s/v .
2 2 K
To determine K, notice that y(w) = 0, since we put the origin at the target point. Then
1 1−s/v 1 1 1+s/v
Kw − w = 0,
2 2 K
s/v
and we obtain K = w . Therefore,
w
x
1−s/v x
1+s/v
y(x) = − .
2 w w
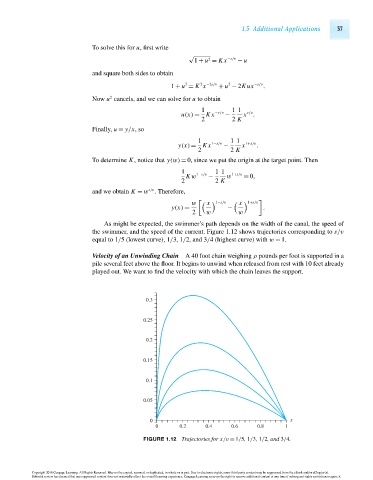
As might be expected, the swimmer’s path depends on the width of the canal, the speed of
the swimmer, and the speed of the current. Figure 1.12 shows trajectories corresponding to s/v
equal to 1/5 (lowest curve), 1/3, 1/2, and 3/4 (highest curve) with w = 1.

Velocity of an Unwinding Chain A 40 foot chain weighing ρ pounds per foot is supported in a
pile several feet above the floor. It begins to unwind when released from rest with 10 feet already
played out. We want to find the velocity with which the chain leaves the support.

0.3

0.25

0.2

0.15

0.1

0.05

0 x
0 0.2 0.4 0.6 0.8 1
FIGURE 1.12 Trajectories for x/v = 1/5, 1/3, 1/2, and 3/4.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:9 THM/NEIL Page-37 27410_01_ch01_p01-42