Page 180 - Aerodynamics for Engineering Students

Two-dimensional wing theoly 163

Y

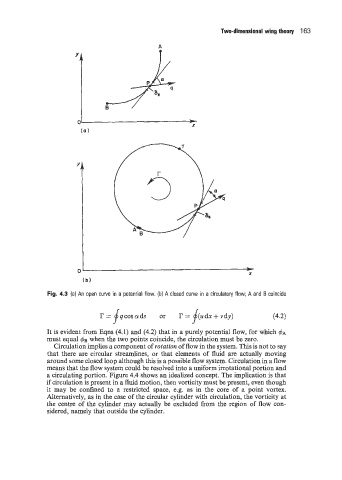
Fig. 4.3 (a) An open curve in a potential flow. (b) A closed curve in a circulatory flow; A and B coincide

It is evident from Eqns (4.1) and (4.2) that in a purely potential flow, for which $A
must equal 4~ when the two points coincide, the circulation must be zero.
Circulation implies a component of rotution of flow in the system. This is not to say
that there are circular streamlines, or that elements of fluid are actually moving
around some closed loop although this is a possible flow system. Circulation in a flow
means that the flow system could be resolved into a uniform irrotational portion and
a circulating portion. Figure 4.4 shows an idealized concept. The implication is that
if circulation is present in a fluid motion, then vorticity must be present, even though
it may be confined to a restricted space, e.g. as in the core of a point vortex.
Alternatively, as in the case of the circular cylinder with circulation, the vorticity at
the centre of the cylinder may actually be excluded from the region of flow con-
sidered, namely that outside the cylinder.