Page 207 - Air pollution and greenhouse gases from basic concepts to engineering applications for air emission control

182 6 Separation of Particles from a Gas

g 4aL
sf
g d p ¼ 1 exp ð6:96Þ
ð 1 aÞpd f
Equation (6.96) shows that we can calculate the fractional efficiency of a filter
with fixed specifications (a; d f ; LÞ as long as the single fiber efficiency is deter-
mined. This equation also shows that the overall filtration efficiency increases over
time as the solidity increases too when particles take more void space in filter.
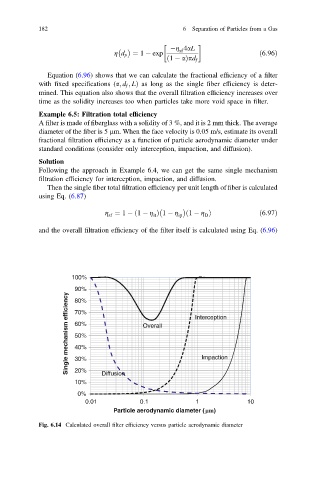
Example 6.5: Filtration total efficiency
A filter is made of fiberglass with a solidity of 3 %, and it is 2 mm thick. The average
diameter of the fiber is 5 µm. When the face velocity is 0.05 m/s, estimate its overall
fractional filtration efficiency as a function of particle aerodynamic diameter under
standard conditions (consider only interception, impaction, and diffusion).

Solution
Following the approach in Example 6.4, we can get the same single mechanism
filtration efficiency for interception, impaction, and diffusion.
Then the single fiber total filtration efficiency per unit length of fiber is calculated
using Eq. (6.87)

g ¼ 1 1 gð it Þ 1 g ip ð 1 g Þ ð6:97Þ
sf
D
and the overall filtration efficiency of the filter itself is calculated using Eq. (6.96)

100%
90%
Single mechanism efficiency 70% Overall Interception
80%

60%
50%
40%
Impaction
30%
20%
Diffusion
10% Diffusion
0%
0.01 0.1 1 10
Particle aerodynamic diameter (µm)
Fig. 6.14 Calculated overall filter efficiency versus particle aerodynamic diameter