Page 212 - Algae

Working with Light 195

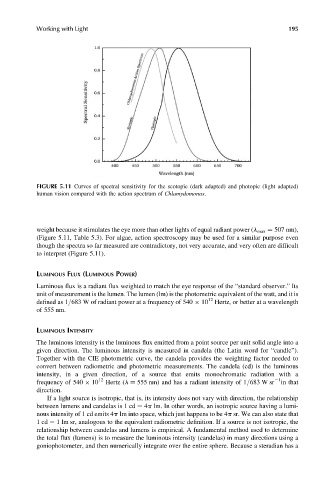
FIGURE 5.11 Curves of spectral sensitivity for the scotopic (dark adapted) and photopic (light adapted)
human vision compared with the action spectrum of Chlamydomonas.

weight because it stimulates the eye more than other lights of equal radiant power (l max ¼ 507 nm),
(Figure 5.11, Table 5.3). For algae, action spectroscopy may be used for a similar purpose even
though the spectra so far measured are contradictory, not very accurate, and very often are difficult
to interpret (Figure 5.11).

LUMINOUS FLUX (LUMINOUS POWER)
Luminous flux is a radiant flux weighted to match the eye response of the “standard observer.” Its
unit of measurement is the lumen. The lumen (lm) is the photometric equivalent of the watt, and it is
12
defined as 1/683 W of radiant power at a frequency of 540 10 Hertz, or better at a wavelength
of 555 nm.

LUMINOUS INTENSITY

The luminous intensity is the luminous flux emitted from a point source per unit solid angle into a
given direction. The luminous intensity is measured in candela (the Latin word for “candle”).
Together with the CIE photometric curve, the candela provides the weighting factor needed to
convert between radiometric and photometric measurements. The candela (cd) is the luminous
intensity, in a given direction, of a source that emits monochromatic radiation with a
frequency of 540 10 12 Hertz (l ¼ 555 nm) and has a radiant intensity of 1/683 W sr 21 in that
direction.
If a light source is isotropic, that is, its intensity does not vary with direction, the relationship
between lumens and candelas is 1 cd ¼ 4p lm. In other words, an isotropic source having a lumi-
nous intensity of 1 cd emits 4p lm into space, which just happens to be 4p sr. We can also state that
1cd ¼ 1 lm sr, analogous to the equivalent radiometric definition. If a source is not isotropic, the
relationship between candelas and lumens is empirical. A fundamental method used to determine
the total flux (lumens) is to measure the luminous intensity (candelas) in many directions using a
goniophotometer, and then numerically integrate over the entire sphere. Because a steradian has a