Page 48 - Anatomy of a Robot

02_200256_CH02/Bergren 4/17/03 11:23 AM Page 33
v a t
x 0.5 a t 2 CONTROL SYSTEMS 33
The simplest second-order mechanical model is a weight hanging from a spring.
Since almost everybody has performed this experiment as a kid, let’s think back to how
this system behaves. We’re going to diagram the behaviors, one at a time, and enumer-
ate the behaviors so we can explain them later once we have the equations:
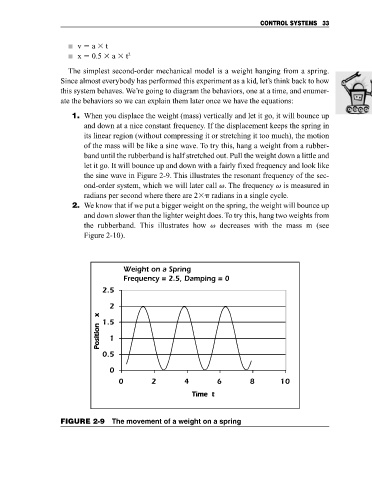
1. When you displace the weight (mass) vertically and let it go, it will bounce up
and down at a nice constant frequency. If the displacement keeps the spring in
its linear region (without compressing it or stretching it too much), the motion
of the mass will be like a sine wave. To try this, hang a weight from a rubber-
band until the rubberband is half stretched out. Pull the weight down a little and
let it go. It will bounce up and down with a fairly fixed frequency and look like
the sine wave in Figure 2-9. This illustrates the resonant frequency of the sec-
ond-order system, which we will later call v. The frequency v is measured in
radians per second where there are 2 radians in a single cycle.
2. We know that if we put a bigger weight on the spring, the weight will bounce up
and down slower than the lighter weight does. To try this, hang two weights from
the rubberband. This illustrates how v decreases with the mass m (see
Figure 2-10).

Weight on a Spring
Frequency = 2.5, Damping = 0
2.5
2
Position x Position x Position x Position x 1.5

1
0.5

0
0 2 4 6 8 10
Time t
Time tTime t
Time t

FIGURE 2-9 The movement of a weight on a spring