Page 50 - Anatomy of a Robot

02_200256_CH02/Bergren 4/17/03 11:23 AM Page 35
CONTROL SYSTEMS 35
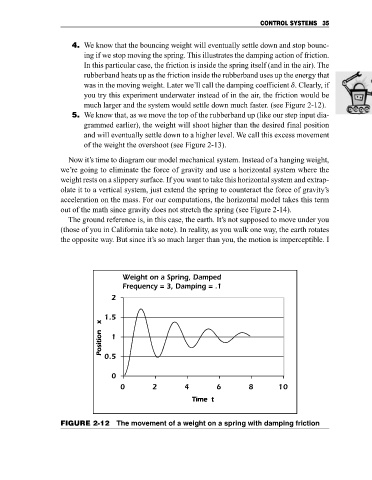
4. We know that the bouncing weight will eventually settle down and stop bounc-
ing if we stop moving the spring. This illustrates the damping action of friction.
In this particular case, the friction is inside the spring itself (and in the air). The
rubberband heats up as the friction inside the rubberband uses up the energy that
was in the moving weight. Later we’ll call the damping coefficient d. Clearly, if
you try this experiment underwater instead of in the air, the friction would be
much larger and the system would settle down much faster. (see Figure 2-12).
5. We know that, as we move the top of the rubberband up (like our step input dia-
grammed earlier), the weight will shoot higher than the desired final position
and will eventually settle down to a higher level. We call this excess movement
of the weight the overshoot (see Figure 2-13).

Now it’s time to diagram our model mechanical system. Instead of a hanging weight,
we’re going to eliminate the force of gravity and use a horizontal system where the
weight rests on a slippery surface. If you want to take this horizontal system and extrap-
olate it to a vertical system, just extend the spring to counteract the force of gravity’s
acceleration on the mass. For our computations, the horizontal model takes this term
out of the math since gravity does not stretch the spring (see Figure 2-14).
The ground reference is, in this case, the earth. It’s not supposed to move under you
(those of you in California take note). In reality, as you walk one way, the earth rotates
the opposite way. But since it’s so much larger than you, the motion is imperceptible. I

Weight on a Spring, Damped
Frequency = 3, Damping = .1
2

1.5
Position x Position x Position x Position x 1

0.5

0
0 2 4 6 8 10
Time t
Time t
Time tTime t
FIGURE 2-12 The movement of a weight on a spring with damping friction