Page 38 - Anthropometry, Apparel Sizing and Design

34 Anthropometry, Apparel Sizing and Design

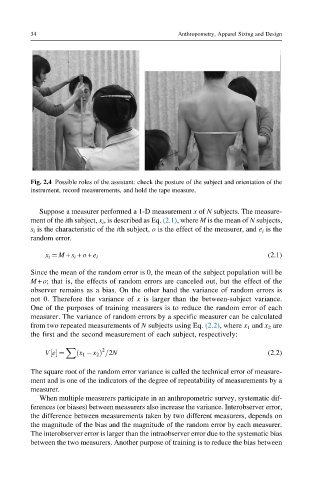
Fig. 2.4 Possible roles of the assistant: check the posture of the subject and orientation of the
instrument, record measurements, and hold the tape measure.

Suppose a measurer performed a 1-D measurement x of N subjects. The measure-
ment of the ith subject, x i , is described as Eq. (2.1), where M is the mean of N subjects,
s i is the characteristic of the ith subject, o is the effect of the measurer, and e i is the
random error.

x i ¼ M + s i + o + e i (2.1)

Since the mean of the random error is 0, the mean of the subject population will be
M+o; that is, the effects of random errors are canceled out, but the effect of the
observer remains as a bias. On the other hand the variance of random errors is
not 0. Therefore the variance of x is larger than the between-subject variance.
One of the purposes of training measurers is to reduce the random error of each
measurer. The variance of random errors by a specific measurer can be calculated
from tworepeatedmeasurementsof N subjects using Eq. (2.2),where x 1 and x 2 are
the first and the second measurement of each subject, respectively:

X 2
Ve½Š ¼ ð x 1 x 2 Þ =2N (2.2)
The square root of the random error variance is called the technical error of measure-
ment and is one of the indicators of the degree of repeatability of measurements by a
measurer.
When multiple measurers participate in an anthropometric survey, systematic dif-
ferences (or biases) between measurers also increase the variance. Interobserver error,
the difference between measurements taken by two different measurers, depends on
the magnitude of the bias and the magnitude of the random error by each measurer.
The interobserver error is larger than the intraobserver error due to the systematic bias
between the two measurers. Another purpose of training is to reduce the bias between