Page 216 - Applied Petroleum Geomechanics

In situ stress estimate 211

e p
r b
u
s p p p T
s i prop r 0
e p
r isip
p p =S p
g c h c
n
i
p
m
u
P
Volume
Volume or time
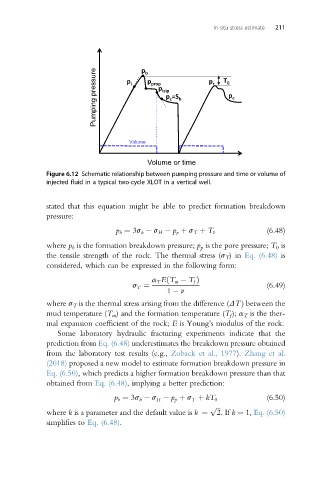
Figure 6.12 Schematic relationship between pumping pressure and time or volume of
injected fluid in a typical two-cycle XLOT in a vertical well.

stated that this equation might be able to predict formation breakdown
pressure:
(6.48)
p b ¼ 3s h s H p p þ s T þ T 0
where p b is the formation breakdown pressure; p p is the pore pressure; T 0 is
the tensile strength of the rock. The thermal stress (s T )in Eq. (6.48) is
considered, which can be expressed in the following form:

a T EðT m T f Þ
s T ¼ (6.49)
1 n
where s T is the thermal stress arising from the difference (DT ) between the
mud temperature (T m ) and the formation temperature (T f ); a T is the ther-
mal expansion coefficient of the rock; E is Young’s modulus of the rock.
Some laboratory hydraulic fracturing experiments indicate that the
prediction from Eq. (6.48) underestimates the breakdown pressure obtained
from the laboratory test results (e.g., Zoback et al., 1977). Zhang et al.
(2018) proposed a new model to estimate formation breakdown pressure in
Eq. (6.50), which predicts a higher formation breakdown pressure than that
obtained from Eq. (6.48), implying a better prediction:

(6.50)
p b ¼ 3s h s H p p þ s T þ kT 0
p ffiffiffi
where k is a parameter and the default value is k ¼ 2.If k ¼ 1, Eq. (6.50)
simplifies to Eq. (6.48).