Page 107 - Applied Statistics And Probability For Engineers

PQ220 6234F.Ch 03 13/04/2002 03:19 PM Page 85

3-8 HYPERGEOMETRIC DISTRIBUTION 85

0.8
N n K
0.7
10 5 5
50 5 25
0.6
50 5 3
0.5
0.4
f (x)
0.3
0.2

0.1
0.0

0 1 2 3 4 5
x
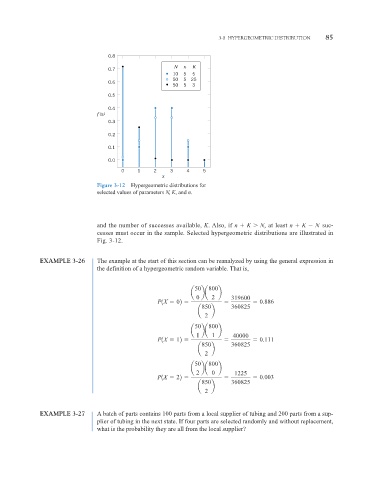
Figure 3-12 Hypergeometric distributions for
selected values of parameters N, K, and n.

and the number of successes available, K. Also, if n K N, at least n K N suc-
cesses must occur in the sample. Selected hypergeometric distributions are illustrated in
Fig. 3-12.

EXAMPLE 3-26 The example at the start of this section can be reanalyzed by using the general expression in
the definition of a hypergeometric random variable. That is,

50 800
a b a b
0 2 319600
P1X 02 0.886
850 360825
a b
2
50 800
a b a b
1 1 40000
P1X 12 0.111
850 360825
a b
2
50 800
a b a b
2 0 1225
P1X 22 0.003
850 360825
a b
2

EXAMPLE 3-27 A batch of parts contains 100 parts from a local supplier of tubing and 200 parts from a sup-
plier of tubing in the next state. If four parts are selected randomly and without replacement,
what is the probability they are all from the local supplier?