Page 171 - Applied statistics and probability for engineers

Section 4-12/Beta Distribution 149

3.0
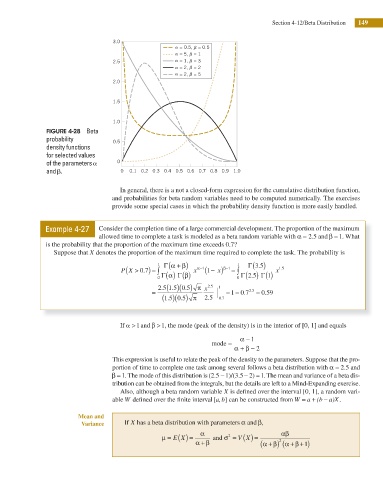
a = 0.5, = 0.5
b
a = 5, = 1
b
2.5 a = 1, = 3
b
b
a = 2, = 2
b
a = 2, = 5
2.0
1.5
1.0
FIGURE 4-28 Beta
probability 0.5
density functions
for selected values
of the parameters a 0
and b. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

In general, there is a not a closed-form expression for the cumulative distribution function,
and probabilities for beta random variables need to be computed numerically. The exercises
provide some special cases in which the probability density function is more easily handled.

Example 4-27 Consider the completion time of a large commercial development. The proportion of the maximum
allowed time to complete a task is modeled as a beta random variable with α = 2.5 and β = 1. What
is the probability that the proportion of the maximum time exceeds 0.7?
Suppose that X denotes the proportion of the maximum time required to complete the task. The probability is
Γ α + β)
.
(
α−
P X > 0 7 . ) = 1 ∫ 0 ( ( x ( 1− x) β− 1 = ∫ 1 0 Γ( Γ( 3 5) 1) ) x 1 5 .
1
2 5 . ) Γ(
Γ α) Γ β ( )

. ( ) . ( ) π x
2 5 . 1 5 0 5 2 5 . 1
= = − . 0 7 . 2 5 = 0 59
.
0
1
. ( ) . ( ) π
1 5 0 5 . 2 5 . 0 7
If a > 1 and β > 1, the mode (peak of the density) is in the interior of [0, 1] and equals
mode = α − 1
α + β − 2
This expression is useful to relate the peak of the density to the parameters. Suppose that the pro-
portion of time to complete one task among several follows a beta distribution with α = 2.5 and
−
=
−
β = 1. The mode of this distribution is (2.5 1)/(3.5 2) 1. The mean and variance of a beta dis-
tribution can be obtained from the integrals, but the details are left to a Mind-Expanding exercise.

Also, although a beta random variable X is deined over the interval [0, 1], a random vari-
able W deined over the i nite interval [a, b ] can be constructed from W = + (b − a)X.
a

Mean and
Variance If X has a beta distribution with parameters α and β,
α αβ
2
μ = ( ) =E X and σ = ( ) =V X
(
α + β ( α + β) α + β + ) 1
2