Page 275 - Autonomous Mobile Robots
P. 275
Adaptive Neural-Fuzzy Control of Mobile Robots 261
1
v
0
v (m/sec) and v (rad/sec) – 2 ω
– 1
– 3
– 4
– 5
– 6
0 0.5 1 1.5 2 2.5 3
Time (sec)
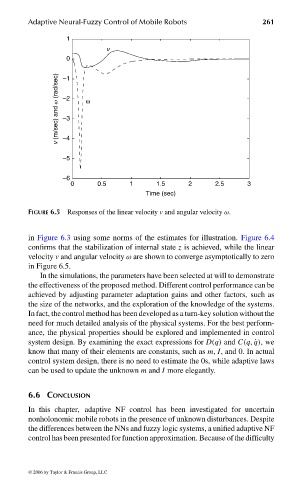
FIGURE 6.5 Responses of the linear velocity v and angular velocity ω.
in Figure 6.3 using some norms of the estimates for illustration. Figure 6.4
confirms that the stabilization of internal state z is achieved, while the linear
velocity v and angular velocity ω are shown to converge asymptotically to zero
in Figure 6.5.
In the simulations, the parameters have been selected at will to demonstrate
the effectiveness of the proposed method. Different control performance can be
achieved by adjusting parameter adaptation gains and other factors, such as
the size of the networks, and the exploration of the knowledge of the systems.
In fact, the control method has been developed as a turn-key solution without the
need for much detailed analysis of the physical systems. For the best perform-
ance, the physical properties should be explored and implemented in control
system design. By examining the exact expressions for D(q) and C(q, ˙q),we
know that many of their elements are constants, such as m, I, and 0. In actual
control system design, there is no need to estimate the 0s, while adaptive laws
can be used to update the unknown m and I more elegantly.
6.6 CONCLUSION
In this chapter, adaptive NF control has been investigated for uncertain
nonholonomic mobile robots in the presence of unknown disturbances. Despite
the differences between the NNs and fuzzy logic systems, a unified adaptive NF
control has been presented for function approximation. Because of the difficulty
© 2006 by Taylor & Francis Group, LLC
FRANKL: “dk6033_c006” — 2006/3/31 — 16:42 — page 261 — #33