Page 135 - Becoming Metric Wise

126 Becoming Metric-Wise

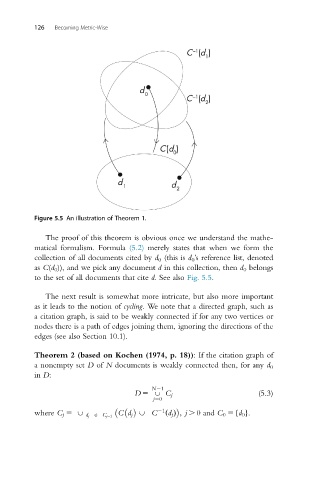
Figure 5.5 An illustration of Theorem 1.

The proof of this theorem is obvious once we understand the mathe-
matical formalism. Formula (5.2) merely states that when we form the
collection of all documents cited by d 0 (this is d 0 ’s reference list, denoted
as C(d 0 )), and we pick any document d in this collection, then d 0 belongs
to the set of all documents that cite d. See also Fig. 5.5.

The next result is somewhat more intricate, but also more important
as it leads to the notion of cycling. We note that a directed graph, such as
a citation graph, is said to be weakly connected if for any two vertices or
nodes there is a path of edges joining them, ignoring the directions of the
edges (see also Section 10.1).

Theorem 2 (based on Kochen (1974, p. 18)): If the citation graph of

a nonempty set D of N documents is weakly connected then, for any d 0
in D:
N21
D 5 , C j (5.3)
j50

21
fg.
Cd j , C ðd j Þ ; j . 0 and C 0 5 d 0
where C j 5 , d j A C j21