Page 406 - Biaxial Multiaxial Fatigue and Fracture

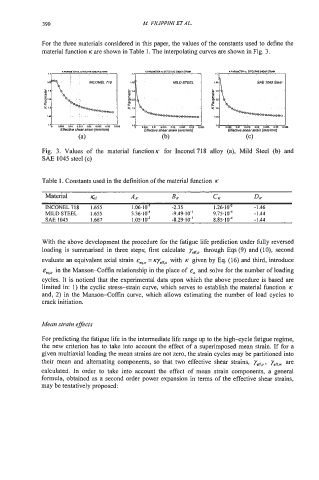
390 M. FILIPPINI ET AL.

For the three materials considered in this paper, the values of the constants used to define the
material function K are shown in Table 1. The interpolating curves are shown in Fig. 3.

SAE 1045 steel

1% OW 00, 0015 om 0 s om om
EIIechresheersnaur[mmfmrn] Ekbve shear strain [mm4nrn] EIIechre shears(rain [mmhn]
(4 (b) (c)
Fig. 3. Values of the material function^ for Inconel 718 alloy (a), Mild Steel (b) and
SAJ? 1045 steel (c)

Table 1. Constants used in the definition of the material fimction K
Material CI A, BK C, DK
INCONEL 71 8 1 655 1.06.10-5 -2.35 1 .26.102 -1.46
MILD STEEL 1.655 3.36.10' -9.49.10' 9.75.104 -1.44
SAE 1045 1.667 1.05.10' -8.29.1 0-' 8.851O4 -1.44

With the above development the procedure for the fatigue life prediction under fully reversed
loading is summarised in three steps; first calculate y&@ through Eqs (9) and (lo), second
evaluate an equivalent axial strain cwp = KY~,~ with K given by Eq. (16) and third, introduce
cwP in the Manson-Cofin relationship in the place of E, and solve for the number of loading
cycles. It is noticed that the experimental data upon which the above procedure is based are
limited in: 1) the cyclic stress-strain curve, which serves to establish the material function K
and, 2) in the Manson-Coffin curve, which allows estimating the number of load cycles to
crack initiation.

Mean strain effects

For predicting the fatigue life in the intermediate life range up to the high-cycle fatigue regime,
the new criterion has to take into account the effect of a superimposed mean strain. If for a
given multiaxial loading the mean strains are not zero, the strain cycles may be partitioned into
their mean and alternating components, so that two effective shear strains, y&#, ye'errm are
calculated. In order to take into account the effect of mean strain components, a general
formula, obtained as a second order power expansion in terms of the effective shear strains,
may be tentatively proposed: