Page 171 - Bio Engineering Approaches to Cancer Diagnosis and Treatment
P. 171
7.5 Hyperthermia 169
FIGURE 7.6 The coercivity changes vs the nanoparticles size.
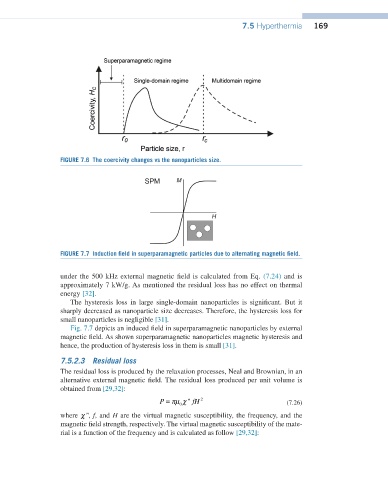
FIGURE 7.7 Induction field in superparamagnetic particles due to alternating magnetic field.
under the 500 kHz external magnetic field is calculated from Eq. (7.24) and is
approximately 7 kW/g. As mentioned the residual loss has no effect on thermal
energy [32].
The hysteresis loss in large single-domain nanoparticles is significant. But it
sharply decreased as nanoparticle size decreases. Therefore, the hysteresis loss for
small nanoparticles is negligible [31].
Fig. 7.7 depicts an induced field in superparamagnetic nanoparticles by external
magnetic field. As shown superparamagnetic nanoparticles magnetic hysteresis and
hence, the production of hysteresis loss in them is small [31].
7.5.2.3 Residual loss
The residual loss is produced by the relaxation processes, Neal and Brownian, in an
alternative external magnetic field. The residual loss produced per unit volume is
obtained from [29,32]:
P πµ χ '' fH 2 (7.26) P=πµ χ’’fH 2
=
0
0
where ''χ , f, and H are the virtual magnetic susceptibility, the frequency, and the χ’’
magnetic field strength, respectively. The virtual magnetic susceptibility of the mate-
rial is a function of the frequency and is calculated as follow [29,32]: