Page 197 - Bio Engineering Approaches to Cancer Diagnosis and Treatment

196 CHAPTER 8 Ultrasound applications in cancer therapy

FIGURE 8.5 Gray section, inner boundary layer (Schlichting) and white section, outer
boundary layer (Rayleigh).

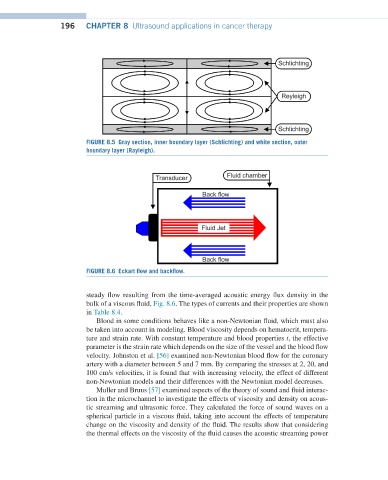
FIGURE 8.6 Eckart flow and backflow.

steady flow resulting from the time-averaged acoustic energy flux density in the
bulk of a viscous fluid, Fig. 8.6. The types of currents and their properties are shown
in Table 8.4.
Blood in some conditions behaves like a non-Newtonian fluid, which must also
be taken into account in modeling. Blood viscosity depends on hematocrit, tempera-
ture and strain rate. With constant temperature and blood properties t, the effective
parameter is the strain rate which depends on the size of the vessel and the blood flow
velocity. Johnston et al. [56] examined non-Newtonian blood flow for the coronary
artery with a diameter between 5 and 7 mm. By comparing the stresses at 2, 20, and
100 cm/s velocities, it is found that with increasing velocity, the effect of different
non-Newtonian models and their differences with the Newtonian model decreases.
Muller and Bruus [57] examined aspects of the theory of sound and fluid interac-
tion in the microchannel to investigate the effects of viscosity and density on acous-
tic streaming and ultrasonic force. They calculated the force of sound waves on a
spherical particle in a viscous fluid, taking into account the effects of temperature
change on the viscosity and density of the fluid. The results show that considering
the thermal effects on the viscosity of the fluid causes the acoustic streaming power