Page 94 - Calc for the Clueless

Newton's Method

Suppose we have an equation y = f(x). Let's say it crosses the x axis at x = r. That is, the root f(r) = 0, but it is
not exact. If we can find f(a) < 0 and f(b) > 0, then if f(x) is continuous, there is a point r such that f(r) = 0, and r
is between a and b. We can use Newton's method.

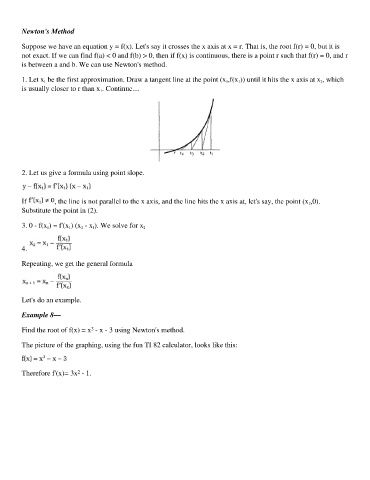
1. Let x 1 be the first approximation. Draw a tangent line at the point (x 1,f(x 1)) until it hits the x axis at x 2, which
is usually closer to r than x 1. Continue....

2. Let us give a formula using point slope.

If , the line is not parallel to the x axis, and the line hits the x axis at, let's say, the point (x 2,0).
Substitute the point in (2).

3. 0 - f(x 1) = f'(x 1) (x 2 - x 1). We solve for x 2

4.

Repeating, we get the general formula

Let's do an example.

Example 8—

3
Find the root of f(x) = x - x - 3 using Newton's method.
The picture of the graphing, using the fun TI 82 calculator, looks like this:

2
Therefore f'(x)= 3x - 1.