Page 91 - Calc for the Clueless

Chapter 6
Odds and Ends

This is the chapter which covers everything we don't want to put in any of the other chapters.

Differentials

The first topic is differentials. One of the wonderful things calculus does is give techniques for approximations.
Since we live in an imperfect world (really?), approximations are very necessary (exact answers are nicest, of
course, but are not usually necessary and sometimes not attainable). Later we will get more sophisticated means
of approximation. This method is usually the first.

Definition

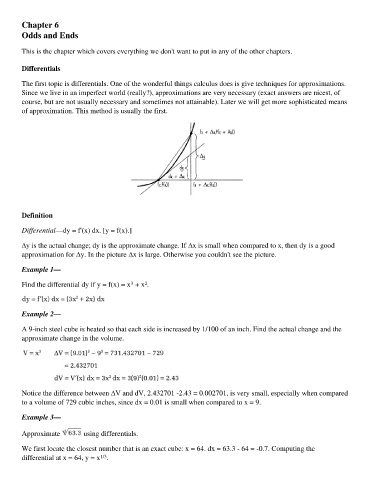
Differential—dy = f'(x) dx. [y = f(x).]

∆y is the actual change; dy is the approximate change. If ∆x is small when compared to x, then dy is a good
approximation for ∆y. In the picture ∆x is large. Otherwise you couldn't see the picture.

Example 1—

2
3
Find the differential dy if y = f(x) = x + x .

Example 2—

A 9-inch steel cube is heated so that each side is increased by 1/100 of an inch. Find the actual change and the
approximate change in the volume.

Notice the difference between ∆V and dV, 2.432701 -2.43 = 0.002701, is very small, especially when compared
to a volume of 729 cubic inches, since dx = 0.01 is small when compared to x = 9.

Example 3—

Approximate using differentials.

We first locate the closest number that is an exact cube: x = 64. dx = 63.3 - 64 = -0.7. Computing the
differential at x = 64, y = x .
1/3