Page 152 - Calculus Demystified

Indeterminate Forms
CHAPTER 5
converges. Since the first integral diverges, we conclude that the original 139
integral diverges as well.
3 −1/3
You Try It: Calculate (2x) dx as an improper integral.
−2
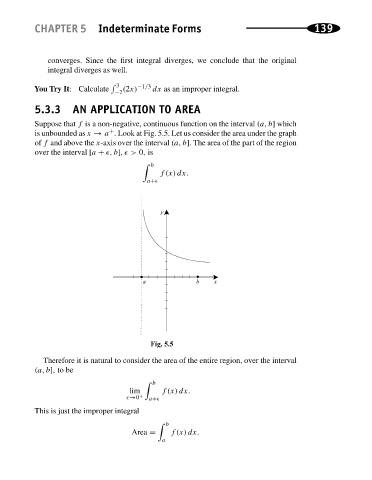
5.3.3 AN APPLICATION TO AREA
Suppose that f is a non-negative, continuous function on the interval (a, b] which
+
is unbounded as x → a . Look at Fig. 5.5. Let us consider the area under the graph
of f and above the x-axis over the interval (a, b]. The area of the part of the region
over the interval [a + (, b],( > 0, is
b

f(x) dx.
a+(

Fig. 5.5
Therefore it is natural to consider the area of the entire region, over the interval
(a, b], to be

b
lim f(x) dx.
(→0 + a+(
This is just the improper integral
b

Area = f(x) dx.
a