Page 257 - Calculus Demystified

CHAPTER 8
244
We partition the interval [a, b]: Applications of the Integral
a = x 0 ≤ x 1 ≤ x 2 ≤ ··· ≤ x k−1 ≤ x k = b.
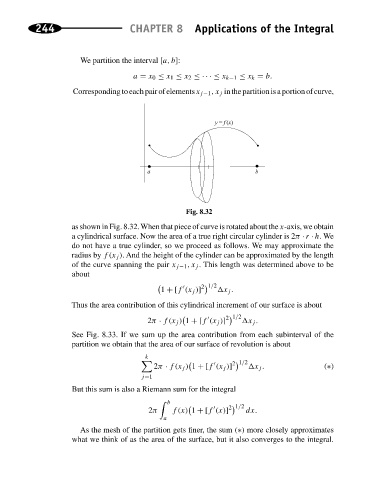
Correspondingtoeachpairofelementsx j−1 ,x j inthepartitionisaportionofcurve,

y = f (x)

a b

Fig. 8.32

as shown in Fig. 8.32.When that piece of curve is rotated about the x-axis, we obtain
a cylindrical surface. Now the area of a true right circular cylinder is 2π · r · h. We
do not have a true cylinder, so we proceed as follows. We may approximate the
radius by f(x j ). And the height of the cylinder can be approximated by the length
of the curve spanning the pair x j−1 ,x j . This length was determined above to be
about

2 1/2
1 +[f (x j )] 8x j .
Thus the area contribution of this cylindrical increment of our surface is about

2 1/2

2π · f(x j ) 1 +[f (x j )] 8x j .
See Fig. 8.33. If we sum up the area contribution from each subinterval of the
partition we obtain that the area of our surface of revolution is about
k

2 1/2

2π · f(x j ) 1 +[f (x j )] 8x j . (∗)
j=1
But this sum is also a Riemann sum for the integral
b

2 1/2

2π f(x) 1 +[f (x)] dx.
a
As the mesh of the partition gets finer, the sum (∗) more closely approximates
what we think of as the area of the surface, but it also converges to the integral.