Page 42 - Calculus Demystified

CHAPTER 1
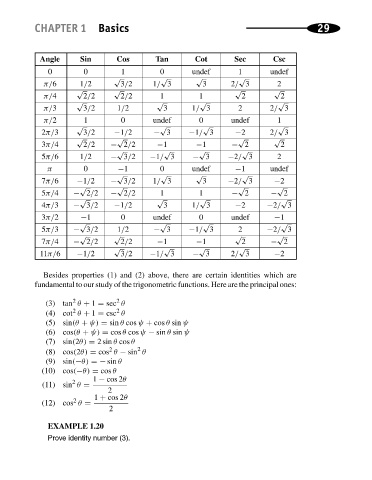
Angle Sin Basics Tan Cot Sec Csc 29
Cos
0 0 1 0 undef 1 undef
√ √ √ √
π/6 1/2 3/2 1/ 3 3 2/ 3 2
√ √ √ √
π/4 2/2 2/2 1 1 2 2
√ √ √ √
π/3 3/2 1/2 3 1/ 3 2 2/ 3
π/2 1 0 undef 0 undef 1
√ √ √ √
2π/3 3/2 −1/2 − 3 −1/ 3 −2 2/ 3
√ √ √ √
3π/4 2/2 − 2/2 −1 −1 − 2 2
√ √ √ √
5π/6 1/2 − 3/2 −1/ 3 − 3 −2/ 3 2
π 0 −1 0 undef −1 undef
√ √ √ √
7π/6 −1/2 − 3/2 1/ 3 3 −2/ 3 −2
√ √ √ √
5π/4 − 2/2 − 2/2 1 1 − 2 − 2
√ √ √ √
4π/3 − 3/2 −1/2 3 1/ 3 −2 −2/ 3
3π/2 −1 0 undef 0 undef −1
√ √ √ √
5π/3 − 3/2 1/2 − 3 −1/ 3 2 −2/ 3
√ √ √ √
7π/4 − 2/2 2/2 −1 −1 2 − 2
√ √ √ √
11π/6 −1/2 3/2 −1/ 3 − 3 2/ 3 −2

Besides properties (1) and (2) above, there are certain identities which are
fundamental to our study of the trigonometric functions. Here are the principal ones:

2
2
(3) tan θ + 1 = sec θ
2
2
(4) cot θ + 1 = csc θ
(5) sin(θ + ψ) = sin θ cos ψ + cos θ sin ψ
(6) cos(θ + ψ) = cos θ cos ψ − sin θ sin ψ
(7) sin(2θ) = 2 sin θ cos θ
2
2
(8) cos(2θ) = cos θ − sin θ
(9) sin(−θ) =− sin θ
(10) cos(−θ) = cos θ
1 − cos 2θ
2
(11) sin θ =
2
1 + cos 2θ
2
(12) cos θ =
2
EXAMPLE 1.20
Prove identity number (3).