Page 75 - Calculus Demystified

CHAPTER 2
Foundations of Calculus
62
(b) lim x→c (f · g) (x) = (lim x→c f(x)) · (lim x→c g(x)) ;

f lim x→c f(x)
(c) lim (x) = provided that lim x→c g(x) = 0;
x→c g lim x→c g(x)
(d) lim x→c (α · f(x)) = α · (lim x→c f(x)) for any constant α.
Some theoretical results, which will prove useful throughout our study of
calculus, are these:
Theorem 2.2
Let a< c < b. A function f on the interval {x : a< x < b} cannot have two
distinct limits at c.

Theorem 2.3
If
lim g(x) = 0
x→c
and
lim f(x) either does not exist or exists and is not zero
x→c
then
f(x)
lim
x→c g(x)
does not exist.

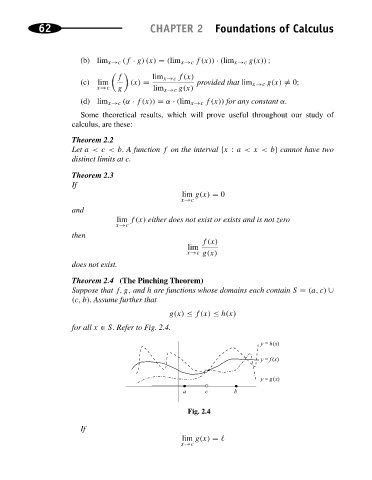
Theorem 2.4 (The Pinching Theorem)
Suppose that f, g, and h are functions whose domains each contain S = (a, c) ∪
(c, b). Assume further that
g(x) ≤ f(x) ≤ h(x)

for all x ∈ S. Refer to Fig. 2.4.

y = h(x)
y = f (x)

y = g(x)

a c b

Fig. 2.4

If
lim g(x) =
x→c