Page 154 - Calculus Workbook For Dummies

138 Part III: Differentiation

Looking Smart with Linear Approximation

Linear approximation is easy to do, and once you get the hang of it, you can impress
your friends by approximating things like 70 in your head — like this: Bingo! 4.125.
3
How did I do it? Look at Figure 8-2 and then at the example to see how I did it.

y
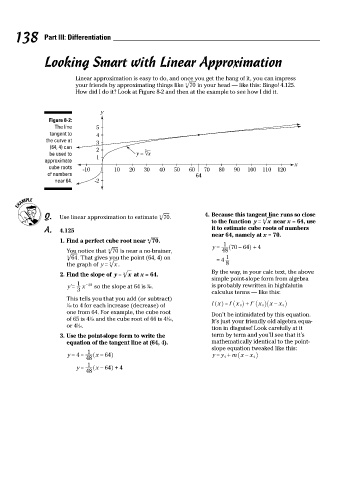
Figure 8-2:
The line 5
tangent to 4
the curve at 3
(64, 4) can 2 3
be used to y = √x
approximate 1
cube roots -10 10 20 30 40 50 60 70 80 90 100 110 120 x
of numbers 64
near 64. -2

Q. Use linear approximation to estimate 70. 4. Because this tangent line runs so close
3
to the function y = 3 x near x = 64, use
A. 4.125 it to estimate cube roots of numbers
near 64, namely at x = 70.
1. Find a perfect cube root near 70.
3
y = 1 ^ 70 - 64 + 4
h
You notice that 70 is near a no-brainer, 48
3
3 64. That gives you the point (64, 4) on = 4 1
the graph of y = 3 x . 8
2. Find the slope of y = 3 x at x = 64. By the way, in your calc text, the above
simple point-slope form from algebra
1 / 2 3
1
y = l x - so the slope at 64 is ⁄48. is probably rewritten in highfalutin
3 calculus terms — like this:
This tells you that you add (or subtract)
f x 0 + l _i
^ h
1 ⁄48 to 4 for each increase (decrease) of l x = _ f x 0 _i x - x 0 i
one from 64. For example, the cube root Don’t be intimidated by this equation.
1
of 65 is 4 ⁄48 and the cube root of 66 is 4 ⁄48, It’s just your friendly old algebra equa-
2
or 4 ⁄24.
1
tion in disguise! Look carefully at it
3. Use the point-slope form to write the term by term and you’ll see that it’s
equation of the tangent line at (64, 4). mathematically identical to the point-
slope equation tweaked like this:
1
4
y - = ^ x - 64h y = y 0 + m x - x 0 i
_
48
1
y = ^ x - 64 + 4
h
48