Page 85 - Calculus for the Clueless, Calc II

Chapter 13—
Odds and Ends

Approximations, Approximations

In an age where computers and calculators—especially those fun graphing calculators—do so many things,
some things cannot be done exactly.

We know that all quadratics can be solved using the quadratic formula. Similarly, there is a cubic formula and a
quartic (4th-degree formula) that can solve all cubics or quartics (although they are truly ugly and messy).
However, in higher mathematics we can prove that most general 5th-degree equations cannot be solved. More
simply, an equation like 2x = cos x cannot be solved exactly. However, we can approximate a solution verrry
closely.

Newton's Method

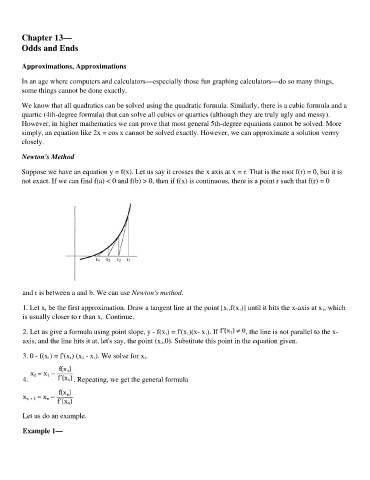
Suppose we have an equation y = f(x). Let us say it crosses the x axis at x = r. That is the root f(r) = 0, but it is
not exact. If we can find f(a) < 0 and f(b) > 0, then if f(x) is continuous, there is a point r such that f(r) = 0

and r is between a and b. We can use Newton's method.

1. Let x 1 be the first approximation. Draw a tangent line at the point [x 1,f(x 1)] until it hits the x-axis at x 2, which
is usually closer to r than x l. Continue.

2. Let us give a formula using point slope, y - f(x 1) = f'(x 1)(x- x 1). If , the line is not parallel to the x-
axis, and the line hits it at, let's say, the point (x 2,0). Substitute this point in the equation given.
3. 0 - f(x 1) = f'(x 1) (x 2 - x 1). We solve for x 2.

4. . Repeating, we get the general formula

Let us do an example.

Example 1—