Page 207 - Carbon Nanotube Fibres and Yarns

Mechanics modeling of carbon nanotube yarns 197

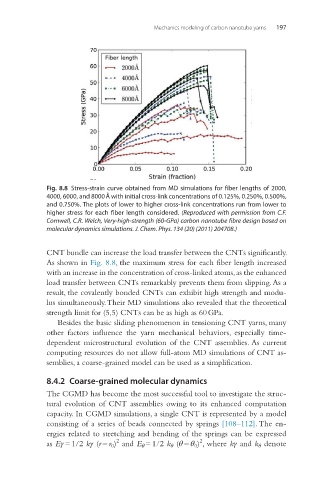
Fig. 8.8 Stress-strain curve obtained from MD simulations for fiber lengths of 2000,
4000, 6000, and 8000 Å with initial cross-link concentrations of 0.125%, 0.250%, 0.500%,
and 0.750%. The plots of lower to higher cross-link concentrations run from lower to
higher stress for each fiber length considered. (Reproduced with permission from C.F.
Cornwell, C.R. Welch, Very-high-strength (60-GPa) carbon nanotube fibre design based on
molecular dynamics simulations. J. Chem. Phys. 134 (20) (2011) 204708.)

CNT bundle can increase the load transfer between the CNTs significantly.
As shown in Fig. 8.8, the maximum stress for each fiber length increased
with an increase in the concentration of cross-linked atoms, as the enhanced
load transfer between CNTs remarkably prevents them from slipping. As a
result, the covalently bonded CNTs can exhibit high strength and modu-
lus simultaneously. Their MD simulations also revealed that the theoretical
strength limit for (5,5) CNTs can be as high as 60 GPa.
Besides the basic sliding phenomenon in tensioning CNT yarns, many
other factors influence the yarn mechanical behaviors, especially time-
dependent microstructural evolution of the CNT assemblies. As current
computing resources do not allow full-atom MD simulations of CNT as-
semblies, a coarse-grained model can be used as a simplification.

8.4.2 Coarse-grained molecular dynamics

The CGMD has become the most successful tool to investigate the struc-
tural evolution of CNT assemblies owing to its enhanced computation
capacity. In CGMD simulations, a single CNT is represented by a model
consisting of a series of beads connected by springs [108–112]. The en-
ergies related to stretching and bending of the springs can be expressed
2
2
as Eγ = 1/2 kγ (r − r 0 ) and E θ = 1/2 k θ (θ − θ 0 ) , where kγ and k θ denote