Page 463 - Chemical process engineering design and economics

442 Chapter 8

After substituting v b v 2, and E from Equations 8.15 and 8.16 into Equation 8.9
and solving for the fluid velocity in the annular area surrounding the float, we find
that

r 2g c (pi-p 2 )/P 1 1/2
(8.17)
2
2
L [(A 0 /A 2 ) /a 2 ]-[(A 0 /A 1 ) /a 1 ] J
By multiplying Equation 8.17 by the annular area, A o, the volumetric flow
rate,

F 2g c (pi-p 2 )/p 1 1/2
= A 0 I - (8.18)
2
2
L [(A 0 /A 2 ) /a 2 ]-[(A 0 /A 1 ) /a 1 ] J
For any flow rate, the float is kept at a stationary position in the fluid by the
drag and buoyant forces acting upwards and the gravitational force acting down-
ward. The force balance is

(8.19)

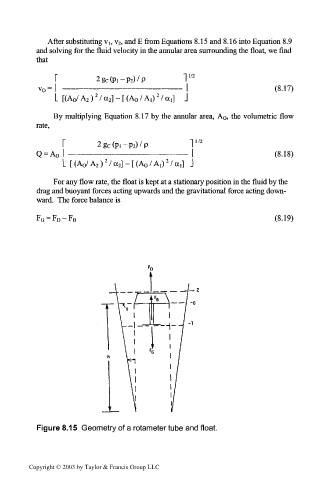
Figure 8.15 Geometry of a rotameter tube and float.

Copyright © 2003 by Taylor & Francis Group LLC