Page 388 - Civil Engineering Formulas

316 CHAPTER TWELVE

V 2
(1 + K e )
2g
H

Hydraulic
grade line

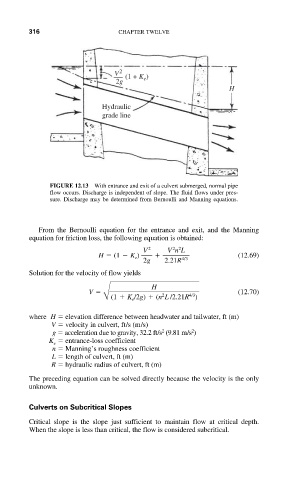
FIGURE 12.13 With entrance and exit of a culvert submerged, normal pipe
flow occurs. Discharge is independent of slope. The fluid flows under pres-
sure. Discharge may be determined from Bernoulli and Manning equations.

From the Bernoulli equation for the entrance and exit, and the Manning
equation for friction loss, the following equation is obtained:
2 2
V 2 V n L
H (1 K e ) (12.69)
2g 2.21R 4/3
Solution for the velocity of flow yields
H
V (12.70)
4/3
2
B(1 K e /2g) (n L /2.21R )
where H elevation difference between headwater and tailwater, ft (m)
V velocity in culvert, ft/s (m/s)
2
2
g acceleration due to gravity, 32.2 ft/s (9.81 m/s )
K entrance-loss coefficient
e
n Manning’s roughness coefficient
L length of culvert, ft (m)
R hydraulic radius of culvert, ft (m)
The preceding equation can be solved directly because the velocity is the only
unknown.

Culverts on Subcritical Slopes
Critical slope is the slope just sufficient to maintain flow at critical depth.
When the slope is less than critical, the flow is considered subcritical.