Page 179 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

168 SUPERVISED LEARNING

1 0.8 1
measure of eccentricity 0.6 measure of eccentricity 0.6
0.8

0.4
0.4
0.2
0 0.2 0
0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1
measure of six-fold rotational symmetry measure of six-fold rotational symmetry

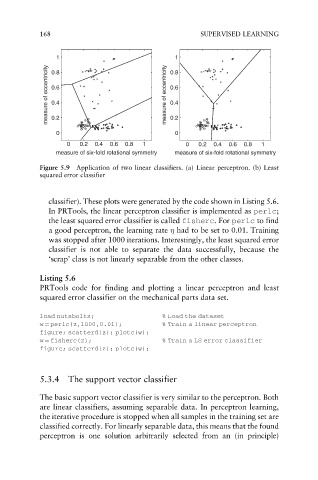
Figure 5.9 Application of two linear classifiers. (a) Linear perceptron. (b) Least
squared error classifier

classifier). These plots were generated by the code shown in Listing 5.6.
In PRTools, the linear perceptron classifier is implemented as perlc;
the least squared error classifier is called fisherc.For perlc to find
a good perceptron, the learning rate had to be set to 0.01. Training
was stopped after 1000 iterations. Interestingly, the least squared error
classifier is not able to separate the data successfully, because the
‘scrap’ class is not linearly separable from the other classes.

Listing 5.6
PRTools code for finding and plotting a linear perceptron and least
squared error classifier on the mechanical parts data set.

load nutsbolts; % Load the dataset
w ¼ perlc(z,1000,0.01); % Train a linear perceptron
figure; scatterd(z); plotc(w);
w ¼ fisherc(z); % Train a LS error classifier
figure; scatterd(z); plotc(w);

5.3.4 The support vector classifier

The basic support vector classifier is very similar to the perceptron. Both
are linear classifiers, assuming separable data. In perceptron learning,
the iterative procedure is stopped when all samples in the training set are
classified correctly. For linearly separable data, this means that the found
perceptron is one solution arbitrarily selected from an (in principle)