Page 204 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

CRITERIA FOR SELECTION AND EXTRACTION 193

respectively. Then, it can be shown that the Chernoff distance
transforms into:

1 T 1
J ðsÞ¼ sð1 sÞðm m Þ ½ð1 sÞC 1 þ sC 2 Š ðm m Þ
2
C
1
2
1
2
" # ð6:19Þ
1 jð1 sÞC 1 þ sC 2 j
þ ln
2 jC 1 j 1 s jC 2 j s
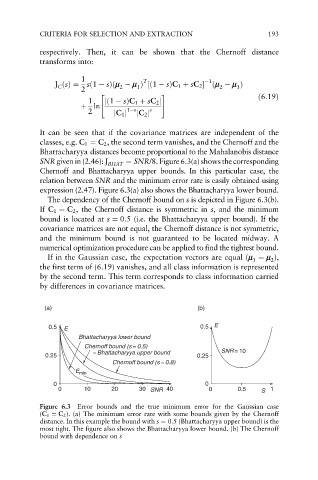
It can be seen that if the covariance matrices are independent of the
classes, e.g. C 1 ¼ C 2 , the second term vanishes, and the Chernoff and the
Bhattacharyya distances become proportional to the Mahalanobis distance
SNR given in (2.46): J BHAT ¼ SNR/8. Figure 6.3(a) shows the corresponding
Chernoff and Bhattacharyya upper bounds. In this particular case, the
relation between SNR and the minimum error rate is easily obtained using
expression (2.47). Figure 6.3(a) also shows the Bhattacharyya lower bound.
The dependency of the Chernoff bound on s is depicted in Figure 6.3(b).
If C 1 ¼ C 2 , the Chernoff distance is symmetric in s, and the minimum
bound is located at s ¼ 0:5 (i.e. the Bhattacharyya upper bound). If the
covariance matrices are not equal, the Chernoff distance is not symmetric,
and the minimum bound is not guaranteed to be located midway. A
numerical optimization procedure can be applied to find the tightest bound.
If in the Gaussian case, the expectation vectors are equal (m ¼ m ),
1
2
the first term of (6.19) vanishes, and all class information is represented
by the second term. This term corresponds to class information carried
by differences in covariance matrices.

(a) (b)

0.5 E 0.5 E
Bhattacharyya lower bound
Chernoff bound (s = 0.5)
= Bhattacharyya upper bound SNR =10
0.25 0.25
Chernoff bound (s = 0.8)
E min
0 0
0 10 20 30 SNR 40 0 0.5 S 1

Figure 6.3 Error bounds and the true minimum error for the Gaussian case
(C 1 ¼ C 2 ). (a) The minimum error rate with some bounds given by the Chernoff
distance. In this example the bound with s ¼ 0:5 (Bhattacharyya upper bound) is the
most tight. The figure also shows the Bhattacharyya lower bound. (b) The Chernoff
bound with dependence on s