Page 77 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

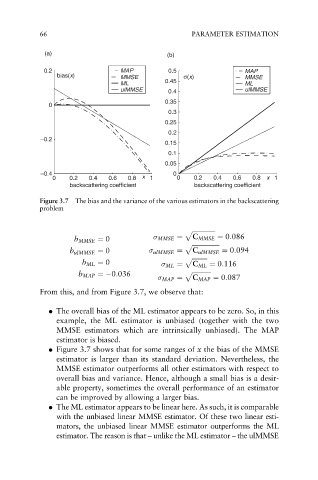
66 PARAMETER ESTIMATION

(a) (b)

0.2 MAP 0.5 MAP
bias(x) MMSE σ(x) MMSE
ML 0.45 ML
ulMMSE 0.4 ulMMSE
0.35
0
0.3
0.25
0.2
–0.2
0.15
0.1
0.05
–0.4 0
0 0.2 0.4 0.6 0.8 x 1 0 0.2 0.4 0.6 0.8 x 1
backscattering coefficient backscattering coefficient
Figure 3.7 The bias and the variance of the various estimators in the backscattering
problem

p ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
b MMSE ¼ 0 MMSE ¼ C MMSE ¼ 0:086
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
b ulMMSE ¼ 0 ulMMSE ¼ C ulMMSE ¼ 0:094
b ML ¼ 0 p ffiffiffiffiffiffiffiffiffiffi
ML ¼ C ML ¼ 0:116
b MAP ¼ 0:036 p ffiffiffiffiffiffiffiffiffiffiffiffi
MAP ¼ C MAP ¼ 0:087
From this, and from Figure 3.7, we observe that:

. The overall bias of the ML estimator appears to be zero. So, in this
example, the ML estimator is unbiased (together with the two
MMSE estimators which are intrinsically unbiased). The MAP
estimator is biased.
. Figure 3.7 shows that for some ranges of x the bias of the MMSE
estimator is larger than its standard deviation. Nevertheless, the
MMSE estimator outperforms all other estimators with respect to
overall bias and variance. Hence, although a small bias is a desir-
able property, sometimes the overall performance of an estimator
can be improved by allowing a larger bias.
. The ML estimator appears to be linear here. As such, it is comparable
with the unbiased linear MMSE estimator. Of these two linear esti-
mators, the unbiased linear MMSE estimator outperforms the ML
estimator. The reason is that – unlike the ML estimator – the ulMMSE