Page 221 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB
P. 221
210 FEATURE EXTRACTION AND SELECTION
T
matrix 1/2 V S b V 1/2 . Let U be a unitary matrix containing the
eigenvectors corresponding to . Then, in the transformed domain
defined by:
1
T
T
y ¼ U V z ð6:47Þ
2
the performance measure becomes:
N 1
X
J INTER=INTRA ¼ traceð Þ¼
i ð6:48Þ
i¼0
T
The operation U corresponds to a rotation of the coordinate system
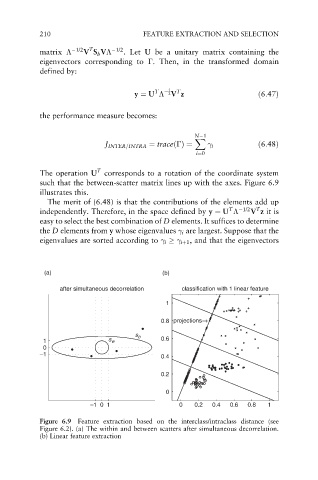
such that the between-scatter matrix lines up with the axes. Figure 6.9
illustrates this.
The merit of (6.48) is that the contributions of the elements add up
T
T
independently. Therefore, in the space defined by y ¼ U 1/2 V z it is
easy to select the best combination of D elements. It suffices to determine
the D elements from y whose eigenvalues
i are largest. Suppose that the
eigenvalues are sorted according to
i
iþ1 , and that the eigenvectors
(a) (b)
after simultaneous decorrelation classification with 1 linear feature
1
0.8 projections→
s b
1 s w 0.6
0
–1 0.4
0.2
0
–1 0 1 0 0.2 0.4 0.6 0.8 1
Figure 6.9 Feature extraction based on the interclass/intraclass distance (see
Figure 6.2). (a) The within and between scatters after simultaneous decorrelation.
(b) Linear feature extraction