Page 178 - Compact Numerical Methods For Computers

One-dimensional problems 167
simulate the operation of the scheme. The results are given in table 13.2. The
arrests are drawn from a uniform distribution on (0,400).

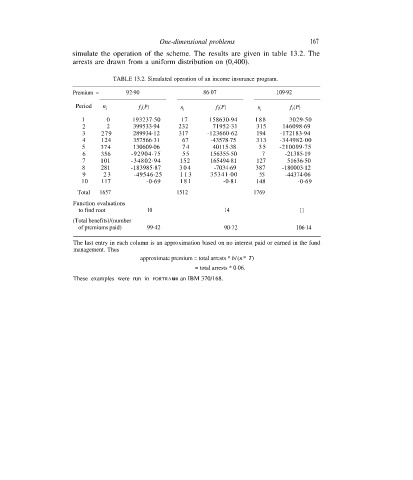
TABLE 13.2. Simulated operation of an income insurance program.
Premium = 92·90 86·07 109·92

Period n j f i (P) n j f i (P) n j f i (P)
1 0 193237·50 17 158630·94 188 3029·50
2 2 399533·94 232 71952·31 315 146098·69
3 279 289934·12 317 -123660·62 194 -172183·94
4 124 357566·31 67 -43578·75 313 -344982·00
5 374 130609·06 74 40115·38 35 -210099·75
6 356 -92904·75 55 156355·50 7 -21385·19
7 101 -34802·94 152 165494·81 127 51636·50
8 281 -183985·87 3 0 4 -7034·69 387 -180003·12
9 2 3 -49546·25 1 1 3 35341·00 55 -44374·06
10 117 -0·69 1 8 1 -0·81 148 -0·69
Total 1657 1512 1769
Function evaluations
to find root 10 14 11
(Total benefits)/(number
of premiums paid) 99·42 90·72 106·14
The last entry in each column is an approximation based on no interest paid or earned in the fund
management. Thus
approximate premium = total arrests * b/(n* T)
= total arrests * 0·06.
These examples were run in FORTRANon an IBM 370/168.