Page 202 - Compact Numerical Methods For Computers

Descent to a minimum I: variable metric algorithms 191

and the coefficients d 1 and d 2 are given by
T
d1=t y (15.35)
and
T
d =(1+y By/d )d . (15.36)
l
2
1
There are several ways in which the update can be computed and added into B. In
practice these may give significantly different convergence patterns due to the
manner in which digit cancellation may occur. However, the author has not been
able to make any definite conclusion as to which of the few ways he has tried is
superior overall. The detailed description in the next section uses a simple
form for convenience of implementation. The properties of the Broyden-
Fletcher-Shanno update will not be discussed further in this work.
In order to start the algorithm, some initial matrix B must be supplied. If it
-1
were easy to compute the Hessian H for the starting parameters b, H would
be the matrix of choice. For general application, however, B=1 n (15.37) is a
simpler choice and has the advantage that it generates the steepest descent
direction in equation (15.29). I have found it useful on a machine having short
mantissa arithmetic to apply the final convergence test on the steepest descent

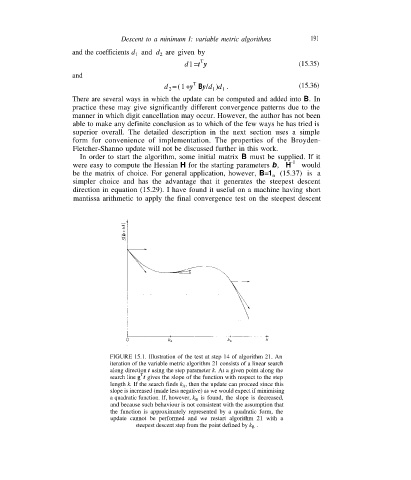
FIGURE 15.1. Illustration of the test at step 14 of algorithm 21. An
iteration of the variable metric algorithm 21 consists of a linear search
along direction t using the step parameter k. At a given point along the
T
search line g t gives the slope of the function with respect to the step
length k. If the search finds k A , then the update can proceed since this
slope is increased (made less negative) as we would expect if minimising
is found, the slope is decreased,
a quadratic function. If, however, k B
and because such behaviour is not consistent with the assumption that
the function is approximately represented by a quadratic form, the
update cannot be performed and we restart algorithm 21 with a
steepest descent step from the point defined by k B .