Page 242 - Compact Numerical Methods For Computers
P. 242
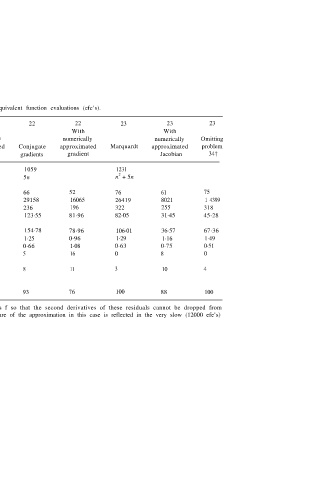
TABLE 18.5. Comparison of algorithm performance as measured by equivalent function evaluations (efe’s).
Algorithm 19+20 21 21 22 22 23 23 23
With With With
numerically numerically numerically Omitting
Type Nelder– Variable approximated Conjugate approximated Marquardt approximated problem
Mead metric gradient gradients gradient Jacobian 34†
Code length† 1242 1068 1059 1231
2
2
2
Array elements n + 4n + 2 n + 5n 5n n + 5n
(a) number of
successful runs 68 68 51 66 52 76 61 75
(b) total efe’s 33394 18292 10797 29158 16065 26419 8021 1 4399
(c) total parameters 230 261 184 236 196 322 255 318
(d) w 1 = (b)/(c) 145·19 70·08 58·68 123·55 81·96 82·05 31·45 45·28
(e) w 0 = average efe’s
per parameter 141·97 76·72 88·25 154·78 78·96 106·01 36·57 67·36
0·98 1·09 1·50 1·25 0·96 1·29 1·16 1·49
(f) r = w 0 /W l
(g) a = 1/(2r – 1) 105 0·84 0·50 0·66 1·08 0·63 0·75 0·51
(h) number of failures 6 3 20 5 16 0 8 0
(i) number of problems
not run 5 8 8 8 11 3 10 4
(j) successes as
percentage of
problems run 92 96 72 93 76 100 88 100
† Problem 34 of the set of 79 has been designed to have residuals f so that the second derivatives of these residuals cannot be dropped from
equation ( 17, 15) to make the Gauss–Newton approximation. The failure of the approximation in this case is reflected in the very slow (12000 efe’s)
convergence of algorithm 23.
‡ On Data General NOVA (23-bit mantissa).