Page 237 - Compact Numerical Methods For Computers

Left-overs 225

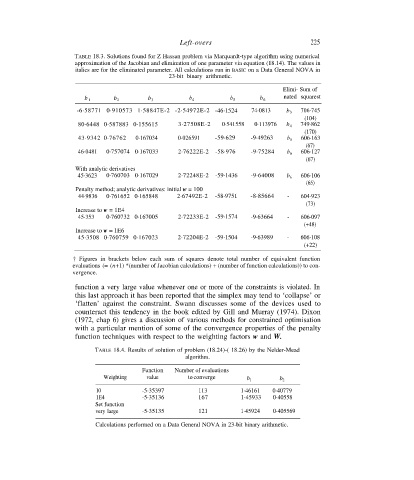
TABLE 18.3. Solutions found for Z Hassan problem via Marquardt-type algorithm using numerical
approximation of the Jacobian and elimination of one parameter via equation (18.14). The values in
italics are for the eliminated parameter. All calculations run in BASIC on a Data General NOVA in
23-bit binary arithmetic.

Elimi- Sum of
nated squarest
b 1 b 2 b 3 b 4 b 5 b 6
-6·58771 0·910573 1·58847E-2 -2·54972E-2 -46·1524 74·0813 b 3 706·745
(104)
80·6448 0·587883 0·155615 3·27508E-2 0·541558 0·113976 b 4 749·862
(170)
43·9342 0·76762 0·167034 0·026591 -59·629 -9·49263 b 5 606·163
(67)
46·0481 0·757074 0·167033 2·76222E-2 -58·976 -9·75284 b 6 606·127
(67)
With analytic derivatives
45·3623 0·760703 0·167029 2·72248E-2 -59·1436 -9·64008 b 6 606·106
(65)
Penalty method; analytic derivatives: initial w = 100
44·9836 0·761652 0·165848 2·67492E-2 -58·9751 -8·85664 - 604·923
(73)
Increase to w = 1E4
45·353 0·760732 0·167005 2·72233E-2 -59·1574 -9·63664 - 606·097
(+48)
Increase to w = 1E6
45·3508 0·760759 0·167023 2·72204E-2 -59·1504 -9·63989 - 606·108
(+22)

† Figures in brackets below each sum of squares denote total number of equivalent function
evaluations (= (n+1) *(number of Jacobian calculations) + (number of function calculations)) to con-
vergence.

function a very large value whenever one or more of the constraints is violated. In
this last approach it has been reported that the simplex may tend to ‘collapse’ or
‘flatten’ against the constraint. Swann discusses some of the devices used to
counteract this tendency in the book edited by Gill and Murray (1974). Dixon
(1972, chap 6) gives a discussion of various methods for constrained optimisation
with a particular mention of some of the convergence properties of the penalty
function techniques with respect to the weighting factors w and W.
TABLE 18.4. Results of solution of problem (18.24)-( 18.26) by the Nelder-Mead
algorithm.

Function Number of evaluations
Weighting value to converge b 1 b 2
10 -5·35397 113 1·46161 0·40779
1E4 -5·35136 167 1·45933 0·40558
Set function
very large -5·35135 121 1·45924 0·405569

Calculations performed on a Data General NOVA in 23-bit binary arithmetic.