Page 232 - Compact Numerical Methods For Computers

-5
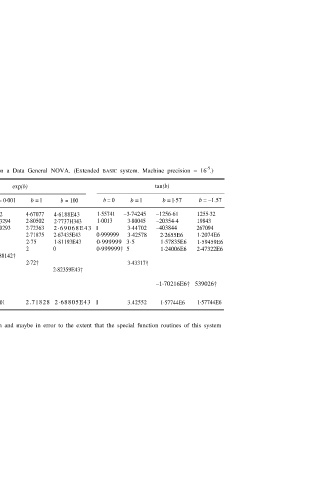
TABLE 18.1. Derivative approximations computed by formula (18.4) on a Data General NOVA. (Extended BASIC system. Machine precision = 16 .)
log(b) exp(b) tan(b)

h b = 0·001 b = 1 b = 100 b = –10 b = 0·001 b = l b = 100 b = 0 b = l b = l·57 b = –1.57

1 6·90876 0·693147 0·95064E–3 7·80101E–5 1·72 4·67077 4·6188E43 1·55741 –3·74245 –1256·61 1255·32
0·0625 66·4166 0·969993 9·99451E–3 4·68483E–5 1·03294 2·80502 2·7737H343 1·0013 3·80045 –20354·4 19843
3·90625E–3 407·171 0·998032 1·00098E–2 4·54858E–5 1·00293 2·72363 2·69068E43 1 3·44702 –403844 267094
2·44141E–4 894·754 0·999756 1·17188E–2 4·52995E–5 1 2·71875 2·67435E43 0·999999 3·42578 2·2655E6 1·2074E6
1·52588E–5 992·437 1 0·0625 4·3869E–5 1 2·75 1·81193E43 0·999999 3·5 1·57835E6 1·59459E6
9·53674E–7 1000 1 0 3·05176E–5 1 2 0 0·999999† 5 1·24006E6 2·47322E6
1·93024E–6 999·012† 0·988142†
9·77516E–4 0·999512† 2·72† 3·43317†
9·76572E–2 9·9999E–3† 2·82359E43†
9·76658E–3 4·56229E–5†
1·53416E–3 –1·70216E6† 539026†
Analytic
derivative‡ 1000 1 0·01 4·54E–5 1.001 2.71828 2·68805E43 1 3.42552 1·57744E6 1·57744E6

† h computed by formula (18.5).
‡ The analytic derivative reported has been evaluated on the NOVA system and maybe in error to the extent that the special function routines of this system
are faulty.