Page 65 - Computational Modeling in Biomedical Engineering and Medical Physics

52 Computational Modeling in Biomedical Engineering and Medical Physics

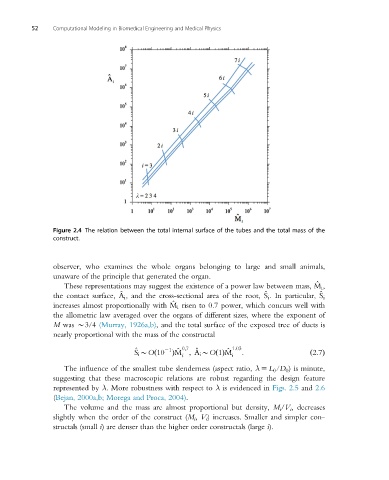
Figure 2.4 The relation between the total internal surface of the tubes and the total mass of the
construct.

observer, who examines the whole organs belonging to large and small animals,
unaware of the principle that generated the organ.
These representations may suggest the existence of a power law between mass, ^ M i ,
^ ^ ^
the contact surface, A i , and the cross-sectional area of the root, S i . In particular, S i
increases almost proportionally with ^ M i risen to 0.7 power, which concurs well with
the allometric law averaged over the organs of different sizes, where the exponent of
M was B3/4 (Murray, 1926a,b), and the total surface of the exposed tree of ducts is
nearly proportional with the mass of the constructal

0;7
^
ˆ
21
S i BOð10 Þ ^ M ; A i BOð1Þ ^ M 1:03 : ð2:7Þ
i
i
The influence of the smallest tube slenderness (aspect ratio, λ 5 L 0 /D 0 ) is minute,
suggesting that these macroscopic relations are robust regarding the design feature
represented by λ. More robustness with respect to λ is evidenced in Figs. 2.5 and 2.6
(Bejan, 2000a,b; Morega and Proca, 2004).
The volume and the mass are almost proportional but density, M i /V i , decreases
slightly when the order of the construct (M i , V i ) increases. Smaller and simpler con-
structals (small i) are denser than the higher order constructals (large i).