Page 86 -

2.7 / KEY TERMS, REVIEW QUESTIONS, AND PROBLEMS 61

a. Determine the effective CPI, MIPS rate, and execution time for each machine.
b. Comment on the results.
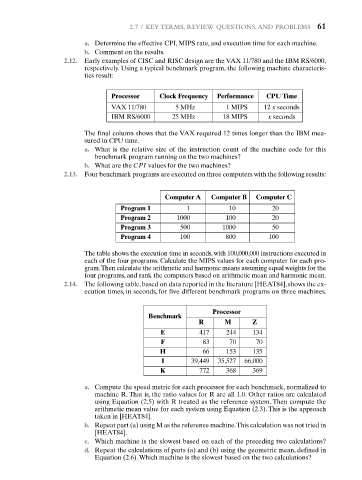
2.12. Early examples of CISC and RISC design are the VAX 11/780 and the IBM RS/6000,
respectively. Using a typical benchmark program, the following machine characteris-
tics result:

Processor Clock Frequency Performance CPU Time
VAX 11/780 5 MHz 1 MIPS 12 x seconds
IBM RS/6000 25 MHz 18 MIPS x seconds
The final column shows that the VAX required 12 times longer than the IBM mea-
sured in CPU time.
a. What is the relative size of the instruction count of the machine code for this
benchmark program running on the two machines?
b. What are the CPI values for the two machines?
2.13. Four benchmark programs are executed on three computers with the following results:

Computer A Computer B Computer C
Program 1 1 10 20
Program 2 1000 100 20
Program 3 500 1000 50
Program 4 100 800 100

The table shows the execution time in seconds, with 100,000,000 instructions executed in
each of the four programs. Calculate the MIPS values for each computer for each pro-
gram.Then calculate the arithmetic and harmonic means assuming equal weights for the
four programs, and rank the computers based on arithmetic mean and harmonic mean.
2.14. The following table, based on data reported in the literature [HEAT84], shows the ex-
ecution times, in seconds, for five different benchmark programs on three machines.

Processor
Benchmark
R M Z
E 417 244 134
F 83 70 70
H 66 153 135
I 39,449 35,527 66,000
K 772 368 369

a. Compute the speed metric for each processor for each benchmark, normalized to
machine R. That is, the ratio values for R are all 1.0. Other ratios are calculated
using Equation (2.5) with R treated as the reference system. Then compute the
arithmetic mean value for each system using Equation (2.3). This is the approach
taken in [HEAT84].
b. Repeat part (a) using M as the reference machine.This calculation was not tried in
[HEAT84].
c. Which machine is the slowest based on each of the preceding two calculations?
d. Repeat the calculations of parts (a) and (b) using the geometric mean, defined in
Equation (2.6).Which machine is the slowest based on the two calculations?