Page 229 - Discrete Mathematics and Its Applications

208 3 / Algorithms

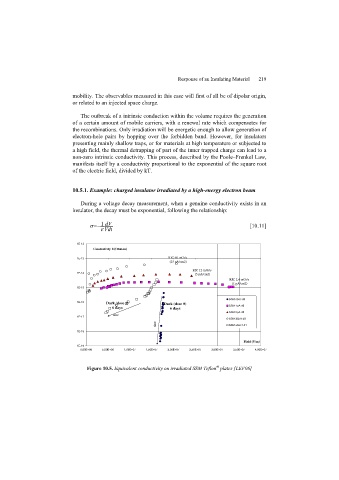
Cg(x)

f (x)

The part of the graph of f (x) that satisfies
f (x)< Cg(x) is shown in color.
g(x)

f (x)< Cg(x) for x > k
k

FIGURE 2 The Function f(x) is O(g(x)).

In subsequent discussions, we will almost always deal with functions that take on only
positive values. All references to absolute values can be dropped when working with big-O
estimates for such functions. Figure 2 illustrates the relationship f(x) is O(g(x)).
Example 2 illustrates how big-O notation is used to estimate the growth of functions.
2
3
EXAMPLE 2 Show that 7x is O(x ).
2
3
Solution:Notethatwhenx> 7,wehave7x <x .(Wecanobtainthisinequalitybymultiplying
2
both sides of x> 7by x .) Consequently, we can take C = 1 and k = 7 as witnesses to establish

DONALD E. KNUTH (BORN 1938) Knuth grew up in Milwaukee, where his father taught bookkeeping at
a Lutheran high school and owned a small printing business. He was an excellent student, earning academic
achievement awards. He applied his intelligence in unconventional ways, winning a contest when he was in the
eighth grade by finding over 4500 words that could be formed from the letters in “Ziegler’s Giant Bar.” This
won a television set for his school and a candy bar for everyone in his class.
Knuth had a difficult time choosing physics over music as his major at the Case Institute of Technology. He
then switched from physics to mathematics, and in 1960 he received his bachelor of science degree, simultane-
ously receiving a master of science degree by a special award of the faculty who considered his work outstanding.
At Case, he managed the basketball team and applied his talents by constructing a formula for the value of each
player. This novel approach was covered by Newsweek and by Walter Cronkite on the CBS television network. Knuth began graduate
work at the California Institute ofTechnology in 1960 and received his Ph.D. there in 1963. During this time he worked as a consultant,
writing compilers for different computers.
Knuth joined the staff of the California Institute of Technology in 1963, where he remained until 1968, when he took a job as a
full professor at Stanford University. He retired as Professor Emeritus in 1992 to concentrate on writing. He is especially interested
in updating and completing new volumes of his series The Art of Computer Programming, a work that has had a profound influence
on the development of computer science, which he began writing as a graduate student in 1962, focusing on compilers. In common
jargon, “Knuth,” referring to The Art of Computer Programming, has come to mean the reference that answers all questions about
such topics as data structures and algorithms.
Knuth is the founder of the modern study of computational complexity. He has made fundamental contributions to the subject of
compilers. His dissatisfaction with mathematics typography sparked him to invent the now widely used TeX and Metafont systems.
TeX has become a standard language for computer typography. Two of the many awards Knuth has received are the 1974 Turing
Award and the 1979 National Medal of Technology, awarded to him by President Carter.
Knuth has written for a wide range of professional journals in computer science and in mathematics. However, his first
publication, in 1957, when he was a college freshman, was a parody of the metric system called “The Potrzebie Systems of Weights
and Measures,” which appeared in MAD Magazine and has been in reprint several times. He is a church organist, as his father was.
He is also a composer of music for the organ. Knuth believes that writing computer programs can be an aesthetic experience, much
like writing poetry or composing music.
Knuth pays $2.56 for the first person to find each error in his books and $0.32 for significant suggestions. If you send him
a letter with an error (you will need to use regular mail, because he has given up reading e-mail), he will eventually inform you
whether you were the first person to tell him about this error. Be prepared for a long wait, because he receives an overwhelming
amount of mail. (The author received a letter years after sending an error report to Knuth, noting that this report arrived several
months after the first report of this error.)