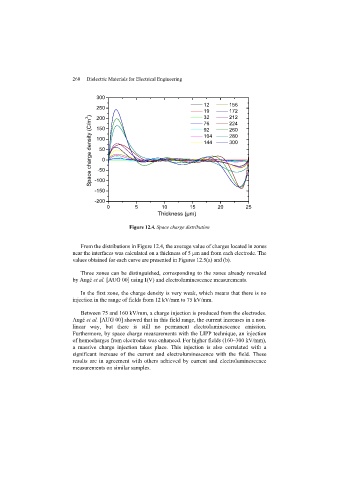
Page 269 - Discrete Mathematics and Its Applications

248 4 / Number Theory and Cryptography

EXAMPLE 5 Find the hexadecimal expansion of (177130) 10 .

Solution: First divide 177130 by 16 to obtain

177130 = 16 · 11070 + 10.

Successively dividing quotients by 16 gives

11070 = 16 · 691 + 14,
691 = 16 · 43 + 3,
43 = 16 · 2 + 11,
2 = 16 · 0 + 2.

The successive remainders that we have found, 10, 14, 3, 11, 2, give us the digits from the right
to the left of 177130 in the hexadecimal (base 16) expansion of (177130) 10 . It follows that

(177130) 10 = (2B3EA) 16 .

(Recall that the integers 10, 11, and 14 correspond to the hexadecimal digits A, B, and E,
respectively.) ▲

EXAMPLE 6 Find the binary expansion of (241) 10 .

Solution: First divide 241 by 2 to obtain

241 = 2 · 120 + 1.

Successively dividing quotients by 2 gives

120 = 2 · 60 + 0,
60 = 2 · 30 + 0,
30 = 2 · 15 + 0,
15 = 2 · 7 + 1,
7 = 2 · 3 + 1,
3 = 2 · 1 + 1,
1 = 2 · 0 + 1.

The successive remainders that we have found, 1, 0, 0, 0, 1, 1, 1, 1, are the digits from the right
to the left in the binary (base 2) expansion of (241) 10 . Hence,

(241) 10 = (1111 0001) 2 . ▲

The pseudocode given in Algorithm 1 finds the base b expansion (a k−1 ...a 1 a 0 ) b of the
integer n.