Page 270 - Discrete Mathematics and Its Applications

4.2 Integer Representations and Algorithms 249

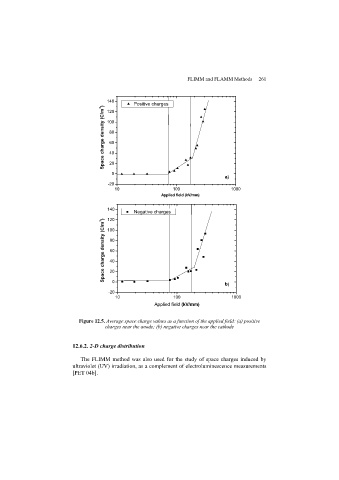
TABLE 1 Hexadecimal, Octal, and Binary Representation of the Integers 0 through 15.
Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F
Octal 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17

Binary 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111

ALGORITHM 1 Constructing Base b Expansions.

procedure base b expansion(n, b: positive integers with b> 1)
q := n
k := 0
while q = 0
a k := q mod b
q := q div b
k := k + 1
return (a k−1 ,...,a 1 ,a 0 ) {(a k−1 ...a 1 a 0 ) b is the base b expansion of n}

In Algorithm 1, q represents the quotient obtained by successive divisions by b, starting with
q = n. The digits in the base b expansion are the remainders of these divisions and are given by
q mod b. The algorithm terminates when a quotient q = 0 is reached.

Remark: Note that Algorithm 1 can be thought of as a greedy algorithm, as the base b digits
are taken as large as possible in each step.

CONVERSION BETWEEN BINARY, OCTAL, AND HEXADECIMAL EXPANSIONS
Conversion between binary and octal and between binary and hexadecimal expansions is ex-
tremely easy because each octal digit corresponds to a block of three binary digits and each
hexadecimal digit corresponds to a block of four binary digits, with these correspondences
shown in Table 1 without initial 0s shown. (We leave it as Exercises 13–16 to show that this is
the case.) This conversion is illustrated in Example 7.

EXAMPLE 7 Find the octal and hexadecimal expansions of (11 1110 1011 1100) 2 and the binary expansions
of (765) 8 and (A8D) 16 .

Solution: To convert (11 1110 1011 1100) 2 into octal notation we group the binary dig-
its into blocks of three, adding initial zeros at the start of the leftmost block if necessary.
These blocks, from left to right, are 011, 111, 010, 111, and 100, corresponding to 3, 7, 2, 7,
and 4, respectively. Consequently, (11 1110 1011 1100) 2 = (37274) 8 . To convert (11 1110 1011
1100) 2 into hexadecimal notation we group the binary digits into blocks of four, adding initial
zeros at the start of the leftmost block if necessary. These blocks, from left to right, are 0011,
1110, 1011, and 1100, corresponding to the hexadecimal digits 3, E, B, and C, respectively.
Consequently, (11 1110 1011 1100) 2 = (3EBC) 16 .
To convert (765) 8 into binary notation, we replace each octal digit by a block of three binary
digits. These blocks are 111, 110, and 101. Hence, (765) 8 = (1 1111 0101) 2 . To convert (A8D) 16
into binary notation, we replace each hexadecimal digit by a block of four binary digits. These
blocks are 1010, 1000, and 1101. Hence, (A8D) 16 = (1010 1000 1101) 2 . ▲