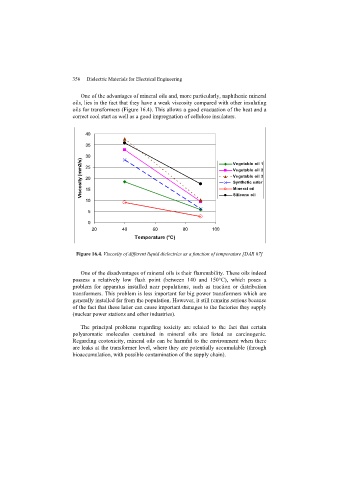
Page 361 - Discrete Mathematics and Its Applications

340 5 / Induction and Recursion

a
b T e T is the triangle abc
p is the vertex of P inside T such that the bap is smallest
p
g bp must be an interior diagonal of P
q d
f

P
c
FIGURE 3 Constructing an Interior Diagonal of a Simple Polygon.

sides of R, because each side of P is a side of either Q or of R, but not both, and the diagonal
ab is a side of both Q and R, but not P . That is, k + 1 = s + t − 2.
We now use the inductive hypothesis. Because both 3 ≤ s ≤ k and 3 ≤ t ≤ k, by the induc-
tive hypothesis we can triangulate Q and R into s − 2 and t − 2 triangles, respectively. Next,
note that these triangulations together produce a triangulation of P . (Each diagonal added to
triangulate one of these smaller polygons is also a diagonal of P .) Consequently, we can trian-
gulate P into a total of (s − 2) + (t − 2) = s + t − 4 = (k + 1) − 2 triangles. This completes
the proof by strong induction. That is, we have shown that every simple polygon with n sides,
where n ≥ 3, can be triangulated into n − 2 triangles.
We now return to our proof of Lemma 1. We present a proof published by Chung-Wu Ho
[Ho75]. Note that although this proof may be omitted without loss of continuity, it does provide
a correct proof of a result proved incorrectly by many mathematicians.

Proof: Suppose that P is a simple polygon drawn in the plane. Furthermore, suppose that b is
the point of P or in the interior of P with the least y-coordinate among the vertices with the
smallest x-coordinate. Then b must be a vertex of P , for if it is an interior point, there would
have to be a vertex of P with a smaller x-coordinate. Two other vertices each share an edge
with b, say a and c. It follows that the angle in the interior of P formed by ab and bc must be
less than 180 degrees (otherwise, there would be points of P with smaller x-coordinates than b).
Now let T be the triangle abc. If there are no vertices of P on or inside T , we can
connect a and c to obtain an interior diagonal. On the other hand, if there are vertices of P
inside T , we will find a vertex p of P on or inside T such that bp is an interior diagonal. (This
is the tricky part. Ho noted that in many published proofs of this lemma a vertex p was found
such that bp was not necessarily an interior diagonal of P . See Exercise 21.) The key is to
select a vertex p such that the angle ∠bap is smallest. To see this, note that the ray starting
at a and passing through p hits the line segment bc at a point, say q. It then follows that the
triangle baq cannot contain any vertices of P in its interior. Hence, we can connect b and p
to produce an interior diagonal of P. Locating this vertex p is illustrated in Figure 3.

Proofs Using the Well-Ordering Property

The validity of both the principle of mathematical induction and strong induction follows from
a fundamental axiom of the set of integers, the well-ordering property (see Appendix 1). The
well-ordering property states that every nonempty set of nonnegative integers has a least element.
We will show how the well-ordering property can be used directly in proofs. Furthermore, it
can be shown (see Exercises 41, 42, and 43) that the well-ordering property, the principle of
mathematical induction, and strong induction are all equivalent. That is, the validity of each of
these three proof techniques implies the validity of the other two techniques. In Section 5.1 we