Page 711 - Discrete Mathematics and Its Applications

690 10 / Graphs

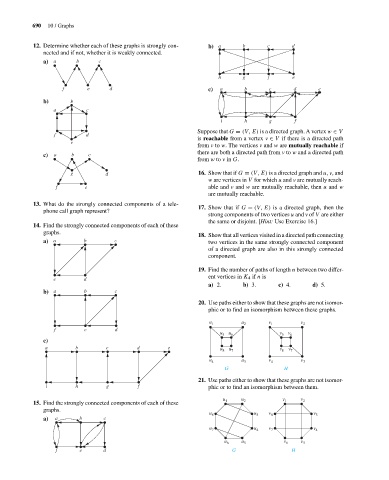
12. Determine whether each of these graphs is strongly con- b) a b c d
nected and if not, whether it is weakly connected.
a) a b c

h g f e
f e d c) a b c d e

b) b
a c

i h g f
Suppose that G = (V, E) is a directed graph. A vertex w ∈ V
f d
is reachable from a vertex v ∈ V if there is a directed path
e
from v to w. The vertices v and w are mutually reachable if
there are both a directed path from v to w and a directed path
c) a b c
from w to v in G.
g d 16. Show that if G = (V, E) is a directed graph and u, v, and
w are vertices in V for which u and v are mutually reach-
f e able and v and w are mutually reachable, then u and w
are mutually reachable.
13. What do the strongly connected components of a tele-
17. Show that if G = (V, E) is a directed graph, then the
phone call graph represent?
strong components of two vertices u and v of V are either
the same or disjoint. [Hint: Use Exercise 16.]
14. Find the strongly connected components of each of these
graphs.
18. Show that all vertices visited in a directed path connecting
a) a b c two vertices in the same strongly connected component
of a directed graph are also in this strongly connected
component.

19. Find the number of paths of length n between two differ-
ent vertices in K 4 if n is
e d
a) 2. b) 3. c) 4. d) 5.
b) a b c
20. Use paths either to show that these graphs are not isomor-
phic or to find an isomorphism between these graphs.
u 1 u 2 v 1 v 2
f e d
u 5 u 6 v 5 v 6
c)
a b c d e u 8 u 7 v 8 v 7

u 4 u 3 v 4 v 3
G H
21. Use paths either to show that these graphs are not isomor-
i h g f phic or to find an isomorphism between them.
u 1 u 2 v 1 v 2
15. Find the strongly connected components of each of these
graphs.
u 8 u 3 v 8 v 3
a) a b c
u 7 u 4 v 7 v 4

u 6 u 5 v 6 v 5
f e d G H