Page 217 - Determinants and Their Applications in Mathematical Physics

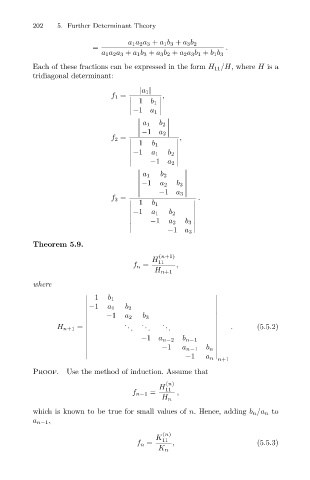
202 5. Further Determinant Theory

a 1 a 2 a 3 + a 1 b 3 + a 3 b 2
= .
a 1 a 2 a 3 + a 1 b 3 + a 3 b 2 + a 2 a 3 b 1 + b 1 b 3
Each of these fractions can be expressed in the form H 11 /H, where H is a
tridiagonal determinant:

|a 1 |
,
f 1 =
1

b 1
−1 a 1

a 1

b 2
−1 a 2

,
f 2 =
1
b 1

−1
a 1
b 2
−1 a 2

a 1 b 2

−1 a 2
b 3
−1 a 3

.
1 b 1
f 3 =
−1 a 1 b 2

−1

a 2 b 3

−1 a 3
Theorem 5.9.
(n+1)
H 11
f n = ,
H n+1
where
1 b 1

−1 a 1 b 2

−1

a 2 b 3
. . .
H n+1 = . . . . . . . (5.5.2)

−1

a n−2 b n−1
−1 a n−1

b n
−1 a n n+1

Proof. Use the method of induction. Assume that
(n)
H 11
f n−1 = H n ,
which is known to be true for small values of n. Hence, adding b n /a n to
a n−1 ,
(n)
K 11
f n = K n , (5.5.3)