Page 318 - Dust Explosions in the Process Industries

Propagation of Flames in Dust Clouds 287

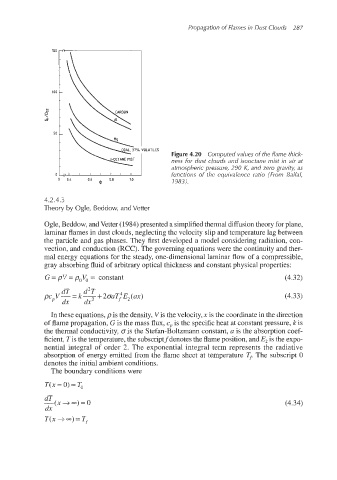
Figure 4.20 Computed values of the flame thick-
ness for dust clouds and isooctane mist in air at
atmospheric pressure, 290 K, and zero gravity, as
functions of the equivalence ratio (From Ballal,
1983).

4.2.4.3
Theory by Ogle, Beddow, and Vetter
Ogle, Beddow, and Vetter (1984)presented a simplifiedthermal diffusion theory for plane,
laminar flames in dust clouds, neglecting the velocity slip and temperature lag between
the particle and gas phases. They first developed a model considering radiation, con-
vection, and conduction (RCC>.The governing equations were the continuity and ther-
mal energy equations for the steady, one-dimensional laminar flow of a compressible,
gray absorbing fluid of arbitrary optical thickness and constant physical properties:
G = pV = poVo= constant (4.32)

dT d2T
pc V-=k-+20aT~E,(ax) (4.33)
dx dx2
In these equations, p is the density, Vis the velocity,x is the coordinatein the direction
of flame propagation, G is the mass flux, cpis the specific heat at constant pressure, k is
the thermal conductivity, ois the Stefan-Boltzmannconstant, a is the absorption coef-
ficient, Tis the temperature, the subscriptfdenotes the flame position, and E2is the expo-
nential integral of order 2. The exponential integral term represents the radiative
absorption of energy emitted from the flame sheet at temperature Tf The subscript 0
denotes the initial ambient conditions.
The boundary conditions were
T(x = 0) = To

dT
-(x -+-) = 0 (4.34)
dX