Page 271 - Dynamic Loading and Design of Structures

Page 242

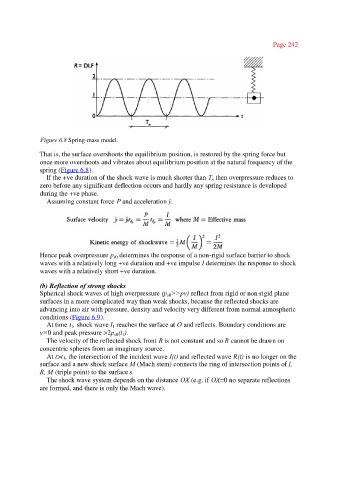
Figure 6.8 Spring-mass model.

That is, the surface overshoots the equilibrium position, is restored by the spring force but
once more overshoots and vibrates about equilibrium position at the natural frequency of the
spring (Figure 6.8).
If the +ve duration of the shock wave is much shorter than T then overpressure reduces to
n
zero before any significant deflection occurs and hardly any spring resistance is developed
during the +ve phase.
Assuming constant force P and acceleration ÿ.

Hence peak overpressure p determines the response of a non-rigid surface barrier to shock
s0
waves with a relatively long +ve duration and +ve impulse I determines the response to shock
waves with a relatively short +ve duration.

(b) Reflection of strong shocks
Spherical shock waves of high overpressure (p >>pv) reflect from rigid or non-rigid plane
s0
surfaces in a more complicated way than weak shocks, because the reflected shocks are
advancing into air with pressure, density and velocity very different from normal atmospheric
conditions (Figure 6.9).
At time t , shock wave I reaches the surface at O and reflects. Boundary conditions are
1
1
v=0 and peak pressure >2p (t ).
s0 1
The velocity of the reflected shock front R is not constant and so R cannot be drawn on
concentric spheres from an imaginary source.
At t>t1, the intersection of the incident wave I(t) and reflected wave R(t) is no longer on the
surface and a new shock surface M (Mach stem) connects the ring of intersection points of I,
R, M (triple point) to the surface s.
The shock wave system depends on the distance OX (e.g. if OX=0 no separate reflections
are formed, and there is only the Mach wave).